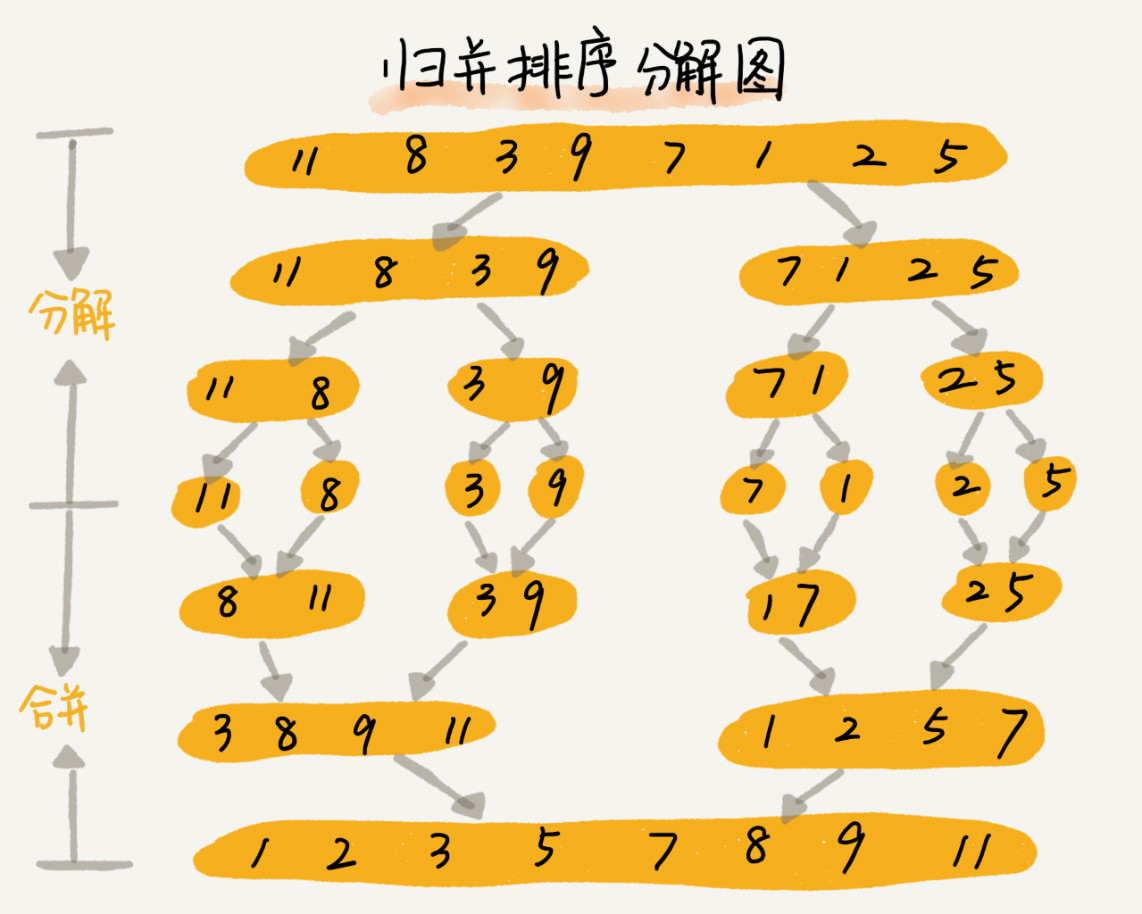
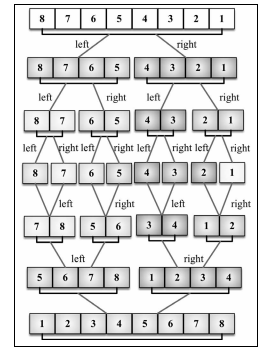
>[success] # 归并算法（还要在好好理解暂时略过） [很不错的文章](https://juejin.im/post/6844904169589964807#heading-0) ~~~ 1.'归并算法'：将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组， 直到最后只有一个排序完毕的大数组 2.如图和定义分析首先需要两步（因此我们需要两个方法）： 2.1.第一个方法是分解需要将大数组不停的切割，直到每个项变成单独一个，这个过程需要一个递归方法 2.2.第二个方法需要合并在比较完成后，将每个小块依次比较最后形成一个大数组 3.上面用到的思想叫'分治思想'。将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了 ~~~  * 引用《数据结构与算法之美》王争老师的图  * 引用《javasprict 数据结构与算法》  >[info] ## 代码实现 * 通用方法 ~~~ // 生成随机数数组 function randomArray(max, min, len) { let randomNum = 0 const array = [] for (let i = 0; i < len; i++) { randomNum = Math.floor((Math.random() * (max - min + 1)) + min) array.push(randomNum) } return array } // const array = randomArray(1, 10, 5) const Compare = { LESS_THAN: -1, BIGGER_THAN: 1, EQUALS: 0 }; function defaultCompare(a, b) { if (a === b) { return Compare.EQUALS; } return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN; } ~~~ >[danger] ##### 代码分析 ~~~ 1.跟上面的分析一样需要两个方法第一个方法是分，也就是将数组分成最小单个为一组数组方法'mergeSort', 第二个就是将这些细分维度的数组依次比较合并'merge'方法，这里要注意的是'merge'方法里面有个暂存 新排序的数组 2.'mergeSort'方法比较好理解就是一个递归过程，这个过程需要将数组项不停拆分成左右结构， 递归的过程之前章节有分析过，要有一个终止条件这个条件就是'归'，这个方法中的'归'就是将数组 已经拆分成最小结构单独项对应代码中'array.length>1' 判断条件 3.'merge'这个合并方法比较复杂这里拆分了三个结构依次对应{1},{2},{3} 3.1.'{1},{2}' -- 数组会被拆分，这里拿出某一刻的拆分，来对这一部分的代码做解释， 当左侧拆分为'[3,6]',右侧拆分为'[4,5,8]'，这时候需要逻辑是右侧数组中的内容依次和左侧数组中的内容 比较，比较完后会放到'merge'方法中的一个暂存数组，形成数据状态为[3,4,5,6]。这里要注意的是{2}， 首先明确 'i'和'j' 不会同时自增，他们是根据比较状态来决定那个自增，这样就可以形成依次比较 3.2.'{3}' -- 当上面将整体数组排序后，将最后剩余值添加到数组末尾 4.这里来个总结版本：归并首先采用的是'分治思想',这类思想很像递归，把大问题拆成小问题，小问题 解决了，大问题最后也就跟着解决了，简单的说就是'逐一击破' 4.1.'逐一击破'我们要做的就是将数组不停切割，切割的原则是数组长度的二分之一，这种切割就会产生 两个数组，我们要做是在切割最小单位及左右数组里面都只有一个值时候开始我们的比较 4.2.'在选排序' 和 '插入排序'的时候这两者用的是，将数组分成两个区域'已排序'和'为排序'两个区域， '归并排序' 我们将不采用这种结构划分，我会用另外一个数组来存储这些排序后的数据 4.3.上两步我们做好了'拆分'和'比较后值应该存放的位置'，现在要解决如何比较左右两个数组值举个例子, 现在有个数组'[6,7,8,1,3,2,5]',经过拆分后他将呈现效果是： [ 7 ] [ 8 ] [ 6 ] [ 7, 8 ] [ 1 ] [ 3 ] [ 2 ] [ 5 ] [ 1, 3 ] [ 2, 5 ] [ 6, 7, 8 ] [ 1, 3, 2, 5 ] 现在要解决的是两个数组之间值的比较，这里采用指针的解决思路，分别有两个指针，最初位置分别为两个 相互比较数组其实位置 4.4.较两个指针所指向的元素，选择相对小的元素放入到合并空间就是我们在4.2位置创建数组， 并移动指针到下一位置，一直重复这个过程，直到某一指针达到序列尾，将另一序列剩下的所有 元素直接复制到合并序列尾 5.整个归并解决思路： 5.1.申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列； 5.2.设定两个指针，最初位置分别为两个已经排序序列的起始位置； 5.3.比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置； 5.4.重复步骤 3 直到某一指针达到序列尾； 5.5.将另一序列剩下的所有元素直接复制到合并序列尾。 ~~~ ~~~ //1.将数组进行切割变成只用单独一项 function mergeSort(array,compareFn = defaultCompare){ // 如果数组只有一项就不用进行比较了 // 这是一个递归方法因此 这判断条件相当于'归' 结束递归过程 if(array.length>1){ const {length} = array const middle = Math.floor(length / 2) const left = mergeSort(array.slice(0,middle),compareFn) const right = mergeSort(array.slice(middle,length),compareFn) // console.log(left,right) // 第二步需要合并将这些单个项进行合并比较 array= merge(left,right,compareFn) } // console.log(array,222) return array } function merge(left, right, compareFn) { let i = 0; let j = 0; const result = []; console.log(left,'left'); console.log(right,'right'); while (i < left.length && j < right.length) { // {1} result.push( compareFn(left[i], right[j]) === Compare.LESS_THAN ? left[i++] : right[j++] // {2} ); } console.log(result,2); const a = result.concat(i < left.length ? left.slice(i) : right.slice(j)); // {3} console.log(a,2222); return a } // console.log(array) console.log(mergeSort([3,6,4,5,8])) ~~~ * 打印效果