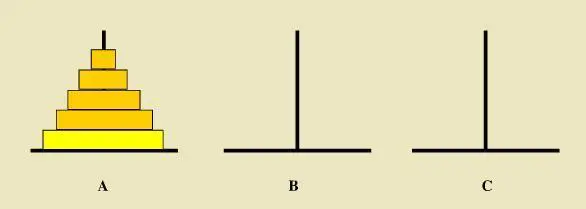
>[success] # 汉诺塔 ~~~ 1.如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到 C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数 ~~~  >[info] ## 栈的思路实现 ~~~~ class Stack { constructor() { this.count = 0; this.items = {}; } push(element) { this.items[this.count] = element; this.count++; } pop() { if (this.isEmpty()) { return undefined; } this.count--; const result = this.items[this.count]; delete this.items[this.count]; return result; } peek() { if (this.isEmpty()) { return undefined; } return this.items[this.count - 1]; } isEmpty() { return this.count === 0; } size() { return this.count; } clear() { /* while (!this.isEmpty()) { this.pop(); } */ this.items = {}; this.count = 0; } toString() { if (this.isEmpty()) { return ''; } let objString = `${this.items[0]}`; for (let i = 1; i < this.count; i++) { objString = `${objString},${this.items[i]}`; } return objString; } } ~~~~ >[danger] ##### 创建一个汉诺塔 ~~~ 1.汉诺塔，是三个柱子为基础，依次是'初始的源柱子上面依次摆放的要移动的盘子'， '辅助的柱子在将盘子转移到目标柱子时候辅助用的'，'目标柱子最后盘子要转移到的柱子' 2.我们将三个柱子看成三个栈，首先要做的就是创建三个柱子，并且个源柱子加上我们要 初始化的盘子 3.关于为什会看成三个栈，首先汉诺塔抽象化，就是一摞东西，无论你怎么操作，只能后进先出， 符合栈的定义，只是变化的是三者每次先后存放位置的顺序 ~~~ ~~~ // 汉诺塔 //---------------------------------------------------------------- // 创建一个汉诺塔 // @params plates 盘子个数 function hanoiStack(plates){ // 用三个栈 对象表示汉诺塔的三个柱子 /* 三个柱子依次表示为 source -- 最初始的柱子 dest -- 要移动到的目标柱子 helper -- 用来辅助移动的中间柱子 */ const source = new Stack(); const dest = new Stack(); const helper = new Stack(); // 给 source 初始柱子 添加初始盘子 // 因为盘子是下往上依次是 for(let i=plates;i>0;i--){ source.push(i) } console.log(source) // 后续需要移动盘子的发方法 return towerOfHanoi(plates, source, helper, dest, 'source', 'helper', 'dest'); } ~~~ >[danger] ##### 移动盘子的方法 -- towerOfHanoi * 选自百度百科 ~~~ 1.当盘子的个数为n时，移动的次数应等于2^n – 1（有兴趣的可以自己证明试试看）。后来一位美国学者发现一种出人 意料的简单方法，只要轮流进行两步操作就可以了。首先把三根柱子按顺序排成品字型，把所有的圆盘按从大到小的 顺序放在柱子A上，根据圆盘的数量确定柱子的排放顺序：若n为偶数，按顺时针方向依次摆放 A B C； 若n为奇数，按顺时针方向依次摆放 A C B。 ⑴按顺时针方向把圆盘1从现在的柱子移动到下一根柱子，即当n为偶数时，若圆盘1在柱子A，则把它移动到B；若圆盘1在柱子B，则把它移动到C；若圆盘1在柱子C，则把它移动到A。 ⑵接着，把另外两根柱子上可以移动的圆盘移动到新的柱子上。即把非空柱子上的圆盘移动到空柱子上，当两根柱子都非空时，移动较大的圆盘。这一步没有明确规定移动哪个圆盘，你可能以为会有多种可能性，其实不然，可实施的行动是唯一的。 ⑶反复进行⑴⑵操作，最后就能按规定完成汉诺塔的移动。 所以结果非常简单，就是按照移动规则向一个方向移动金片： 如3阶汉诺塔的移动：A→C,A→B,C→B,A→C,B→A,B→C,A→C ~~~  ~~~ /* 汉诺塔有三种情况其中两种是极端情况 1.第一种就是源柱没有盘子 相当于直接成功 2.第二种就是源柱只有一个盘子，直接移动一次就可以 3.非极端情况就是有一个以上的盘子需要我们平凡操作 */ function towerOfHanoi(plates,source, helper, dest,helperName, sourceName, destName,moves=[]){ // 没有盘子就一次都不用移动，直接返回空 if(plates === 0) { return moves }else if(plates === 1){ // 直接将第一个移动到第三个 dest.push(source.pop()) const move = {} move[sourceName] = source.toString() move[helperName] = helper.toString() move[destName] = dest.toString() }else{ // 最复杂的多个盘子时候 // 三个柱子 看成动态，不在是固定功能位置 towerOfHanoi(plates - 1, source, dest, helper, sourceName, destName, helperName, moves); dest.push(source.pop()); const move = {}; move[sourceName] = source.toString(); move[helperName] = helper.toString(); move[destName] = dest.toString(); moves.push(move); towerOfHanoi(plates - 1, helper, source, dest, helperName, sourceName, destName, moves); } return moves; } hanoiStack(3) ~~~ * 打印结果  * A→C,A→B,C→B,A→C,B→A,B→C,A→C ~~~ function hanoi(plates, source, helper, dest, moves = []) { if (plates <= 0) { return moves; } if (plates === 1) { moves.push([source, dest]); } else { hanoi(plates - 1, source, dest, helper, moves); moves.push([source, dest]); hanoi(plates - 1, helper, source, dest, moves); } return moves; } console.log(hanoi(3, 'A', 'B', 'C')); ~~~