>[success] # 创建堆 ~~~ 1.创建堆类的方法说明 1.1.getLeftIndex -- 获取左侧节点对应数组实际位置 1.2.getRightIndex -- 获取右侧节点对应数组实际位置 1.3.getParentIndex -- 获取父节点对应数组实际位置 1.4.size -- 堆的大小 1.5.isEmpty -- 堆是否为空 1.6.clear -- 清除堆 1.7.findMinimum -- 求出堆的最小值这里指是最小堆类，最大堆最小堆根接地是对应最大值最小值 1.8.insert -- 堆中插入数据 1.9.siftUp -- 插入数据的比较方法 1.10.extract -- 移除最小堆的最小值 1.11.siftDown -- 从上向下比较进行交换找到最小值 1.12.heapify -- 堆化一个数组 ~~~ >[info] ## 代码实现 -- 最小堆 ~~~ 1.'siftUp' 上移操作方法说明，当往堆中插入一个元素后，将元素插入数组末尾，依次让该元素和其父节点 进行比较，根据创建的大小堆来决定是否和父节点更换位置 -- '当做堆的插入时候用这个思想' 2.'siftDown' 从上向下比较进行交换找到最小值 -- '当做删除的时候用这个思想，这里的删除指的是删除最大或最小' 3.'heapify' 数组堆化，实际只要将非叶子节点，进行堆化后自然就形成了堆，因此循环是二分之一 ~~~ * siftUp 图解  * 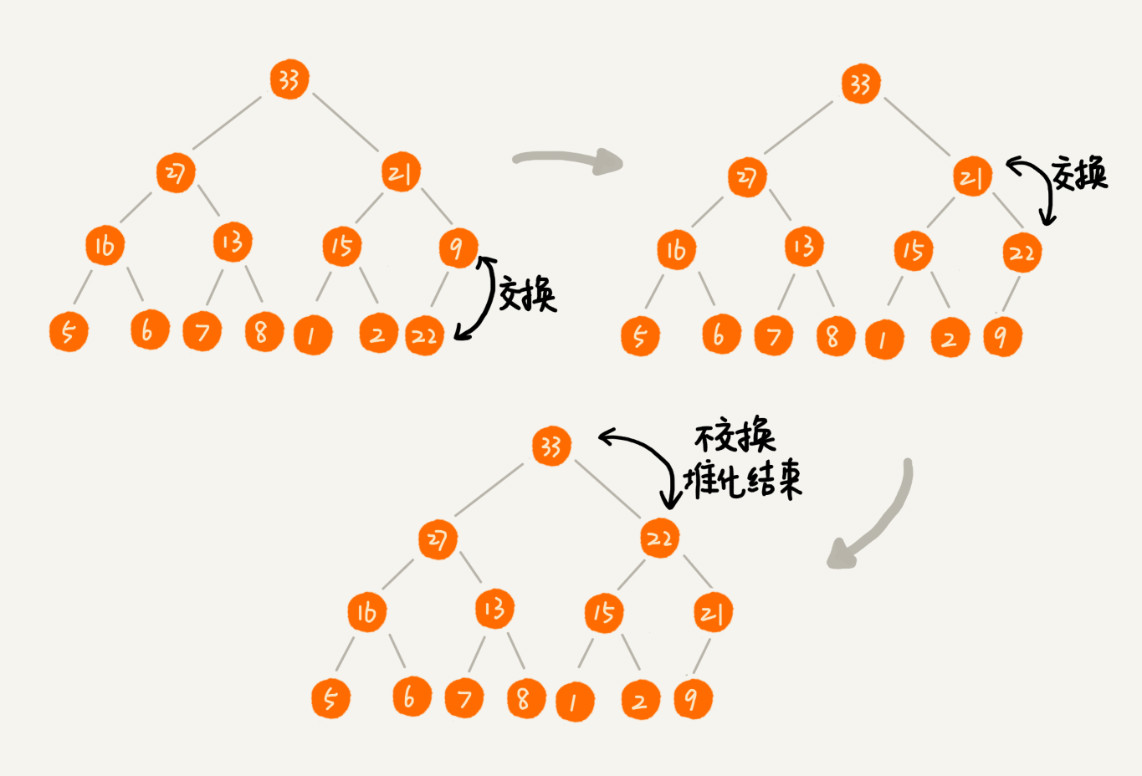siftDown 图解  * 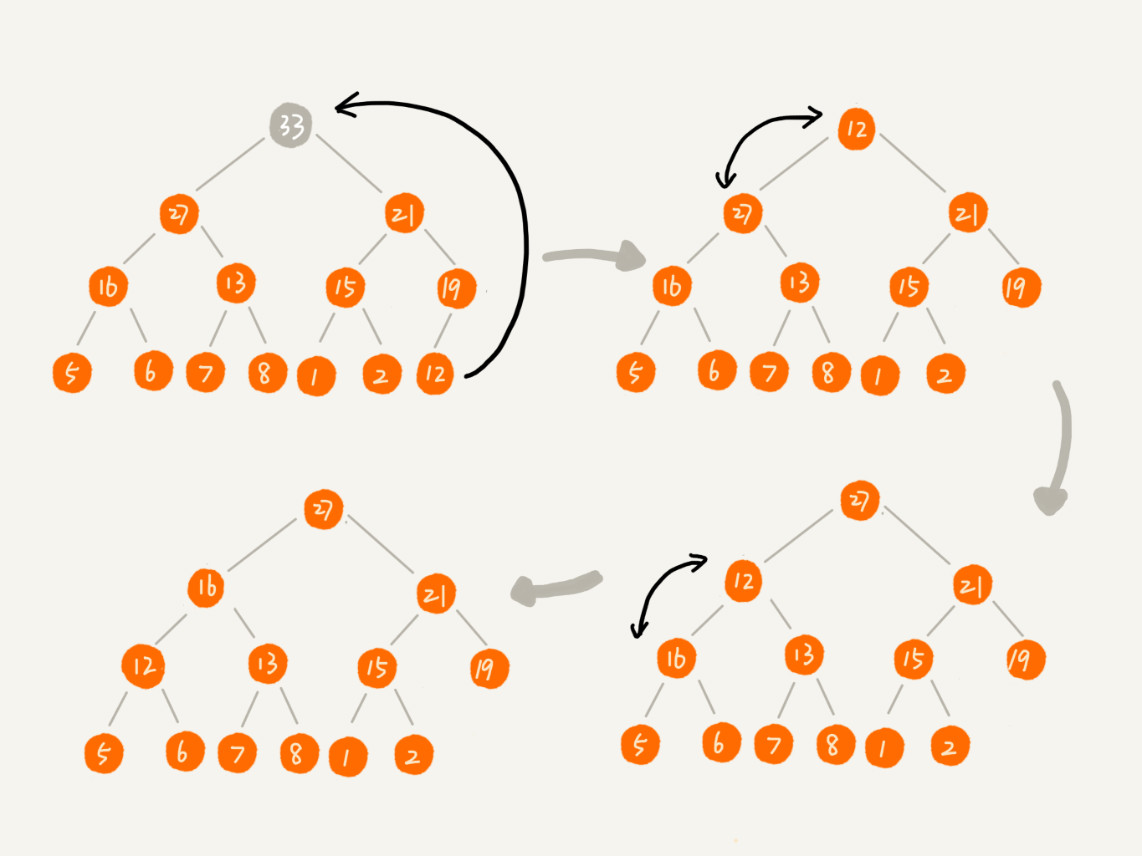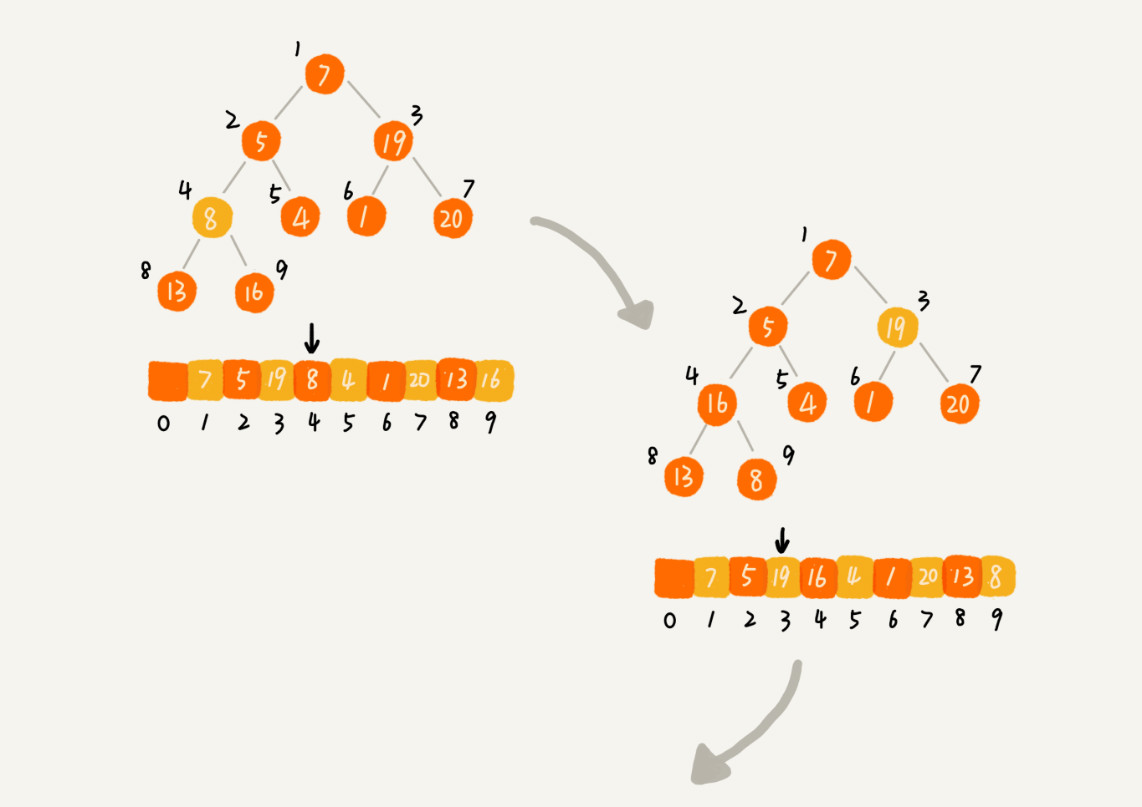heapify 图解 ~~~ 1.二叉堆用的是数组的形式，我们想把一个数组变成堆，最简单的方法，我们循环这个数组一次通过siftUp 插入数组中的 数据 2.第二种就是将整个数组先看成树，然后将树这个树 拆分成小树，这些小树通过'siftDown'进行重新排序， 这里要说明的是我们'siftDown'是一个抽离方法，他其实是根节点和下面的子节点进行比较 3.堆的长度的一半是个个根节点，我们有这些数据分成小树，这些小的树堆化后就会形成大的树 ~~~   ~~~ 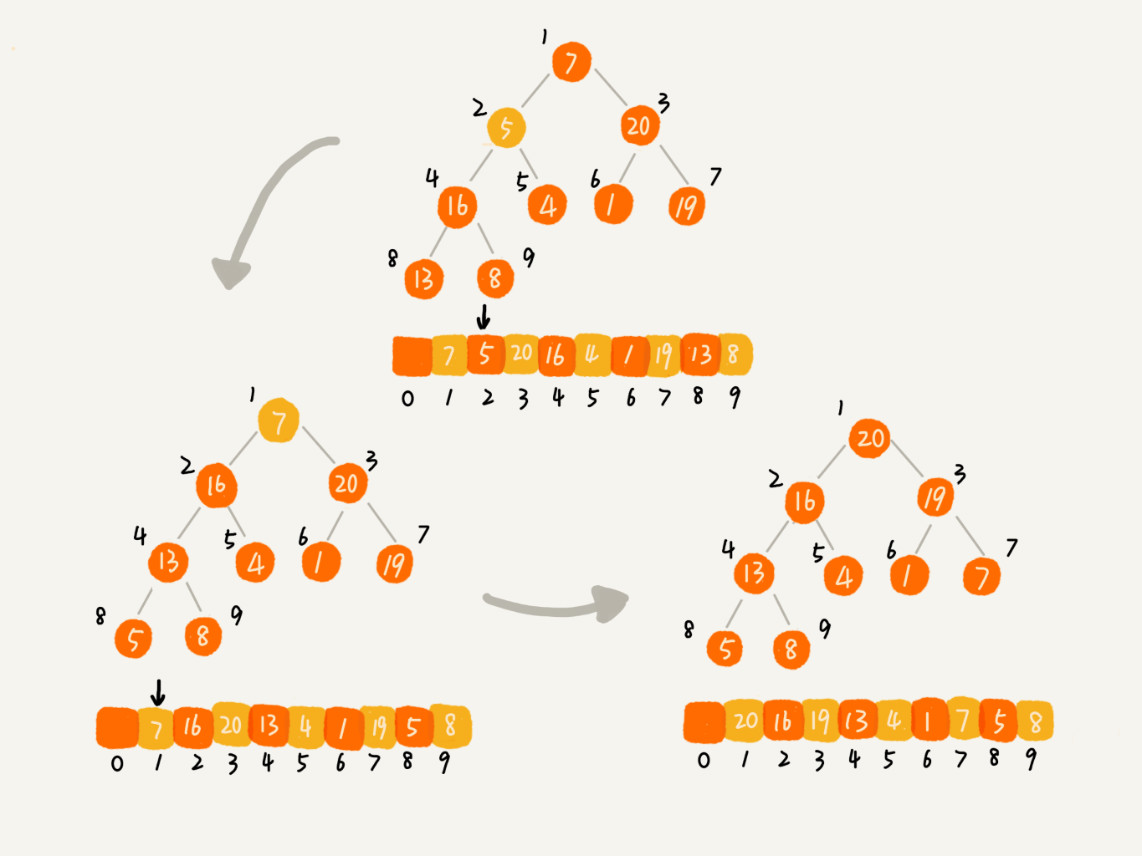1.'说明': 首先我们针对的是二叉堆操作，其次我们一直遵循'siftUp'这种插入规则所以依次比较父节点是没问题的 2.'siftUp' -- 对应插入 3.'siftDown' -- 对应的是删除。因为二叉堆要不就最大堆，要不就是最小堆，这里的删除指的是删除堆顶 ~~~ ~~~ const Compare = { LESS_THAN: -1, BIGGER_THAN: 1, EQUALS: 0 }; function defaultCompare(a, b) { if (a === b) { return Compare.EQUALS; } return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN; } function reverseCompare(compareFn) { return (a, b) => compareFn(b, a); } function swap(array, a, b) { /* const temp = array[a]; array[a] = array[b]; array[b] = temp; */ [array[a], array[b]] = [array[b], array[a]]; } class MinHeap { constructor(compareFn = defaultCompare) { this.compareFn = compareFn; this.heap = [] } // 计算左侧节点数在数组对应位置 getLeftIndex(index) { return (2 * index) + 1 } // 计算右侧节点数组对应位置 getRightIndex(index) { return (2 * index) + 2 } // 计算父节点位置 getParentIndex(index) { if (index === 0) { return undefined } return Math.floor((index - 1) / 2) } // 计算堆得大小 size() { return this.heap.length } // 判断是否为空 isEmpty() { return this.size() <= 0 } // 清空堆 clear() { this.heap = [] } // 找到堆的最小值，因为这是最小堆，所以根节点是最小的 findMinimum() { return this.isEmpty ? undefined : this.heap[0] } // 插入 insert(value) { // 插入的时候判断不能插入为空 if (value != null) { const index = this.heap.length this.heap.push(value) this.siftUp(index) return true } return false } // 插入数据 siftUp(index) { let parent = this.getParentIndex(index) // 从下向上和自己的父节点进行比较，来换彼此位置 while (index > 0 && this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN) { swap(this.heap, parent, index); index = parent parent = this.getParentIndex(index) } } // 移除最小堆的最小值 extract() { // 分情况讨论，当前堆数据空，当前堆数据只有一个，当前堆数据有多个 if (this.isEmpty()) { return undefined } if (this.size() === 1) { return this.heap.shift() } const romevedValue = this.heap[0] // 并且把数组最后一项移到头部 this.heap[0] = this.heap.pop() // 进行比较换位选出实际最小的为数组的第一位 this.siftDown(0) return romevedValue } // 从上向下比较进行交换找到最小值 siftDown(index) { /* 1.思路就是知道当前值 和当前值和叶子节点关系大小，因为这是二叉树 所以也就是相当于比较左右叶子节点先获取，当前值 即当前值左右叶子节点 在数组中的位置 */ let element = index // 当前值的位置 let left = this.getLeftIndex(index) // 当期值的左节点 let right = this.getRightIndex(index) // 当前值的右节点 const size = this.size(); /* 1.比较的思路，因为在比较过程中会不停的更换两个节点的位置，即到最 后节点的位置就将是数组的最后一位，如果比较的过程中已经是最后一位了 说明树已经全部比较完毕 2.当然也要比较当前节点和左右节点的关系 */ if (left < size && this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN) { element = left; } if (right < size && this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN) { element = right; } // 什么继续递归？当 index 也就无法在改变element 值的时候，即已经 // 到了数组末端 index 和 element 相等就无非递归，反之就继续递归 if (index !== element) { swap(this.heap, index, element); this.siftDown(element); } } // 堆化数组 ，查分成小的组合成大 heapify(array) { if (array) { this.heap = array; } const maxIndex = Math.floor(this.size() / 2) - 1; for (let i = 0; i <= maxIndex; i++) { this.siftDown(i); } return this.heap; } getAsArray() { return this.heap; } } let heap = new MinHeap(); heap.insert(2); heap.insert(3); heap.insert(4); heap.insert(5); heap.insert(2); console.log(heap.getAsArray()); console.log(heap.heapify([2, 5, 7, 8, 9, 1, 4, 3])); ~~~ >[info] ## 代码实现 -- 最大堆 ~~~ class MaxHeap extends MinHeap { constructor(compareFn = defaultCompare) { super(compareFn); this.compareFn = compareFn; this.compareFn = reverseCompare(compareFn); } } ~~~