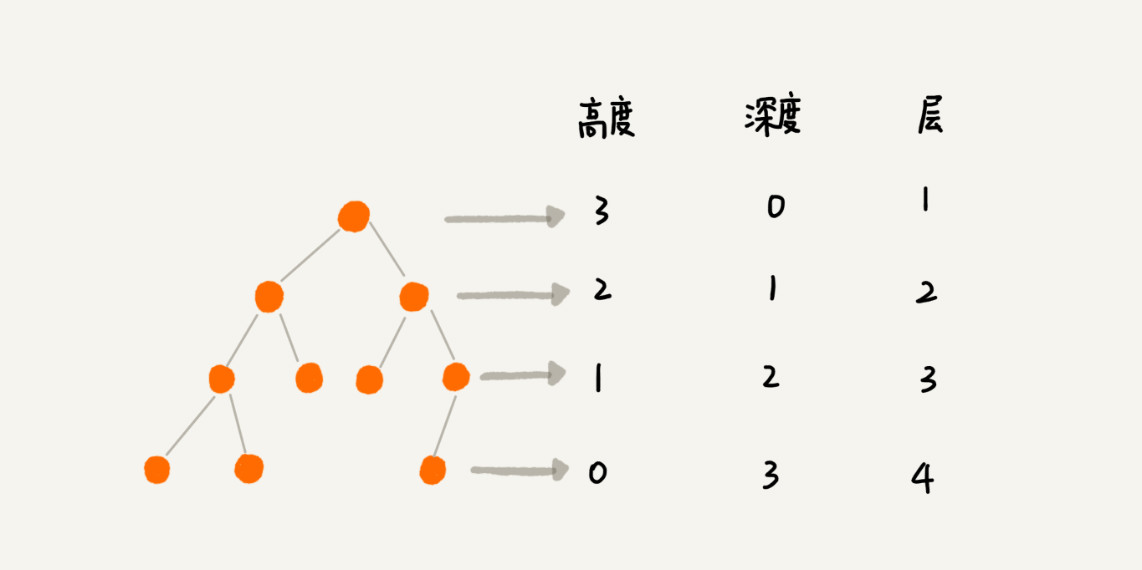
[TOC] >[success] # 树 ~~~ 1.树--是一种非顺序结构 ~~~ >[info] ## 树的相关术语 ~~~ 1.树中每个元素我们叫做'节点'，用来连接相邻'节点'之间的关系，叫做'父子节点' 2.每一个'树结构'都包含一系列存在的父子关系节点，每个节点都有一个'父节点'(除了顶部第一个节点)， 以及0个或多个子节点 3.位于树的顶部的节点叫作'根节点',也可以说把没有父节点的节点叫作'根节点'。至少有一个子节点的节点叫 '内部节点'，没有子元素的节点称为'外部节点'又叫'叶子节点' 4.树还有三个定义：'高度（Height）'、'深度（Depth）'、'层（Level）' ~~~ * 引用数据结构与算法文章的图   >[success] # 二叉树 和 二叉搜索树 ~~~ 1.二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。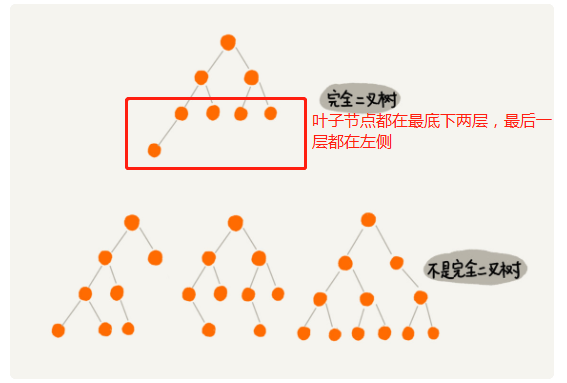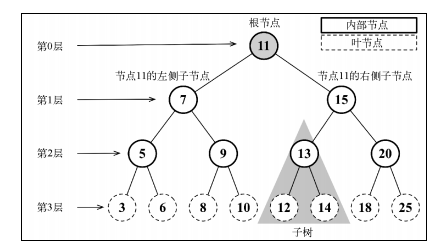注意这里说的 最多的意思是'二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点' 2.关于'满二叉树'，'完全二叉树' 2.1.除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作'满二叉树' 2.2.叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最 大，这种二叉树叫作'完全二叉树' 3.二叉搜索树（BST）是二叉树的一种，但是只允许你在左侧节点存储（比父节点）小的值， 在右侧节点存储（比父节点）大的值。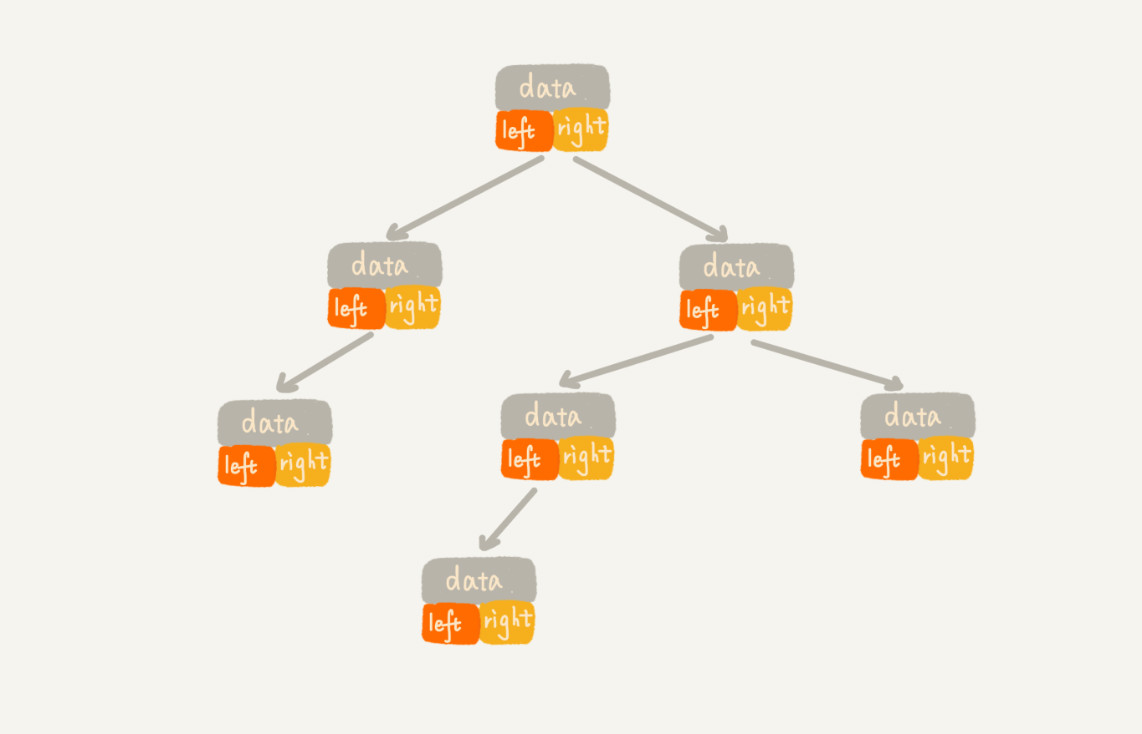 ~~~ * 完全二叉树 和 不完全二叉树  * 二叉搜索树  >[info] ## 链式存储法 -- 实现一个二叉树 ~~~ 1.每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。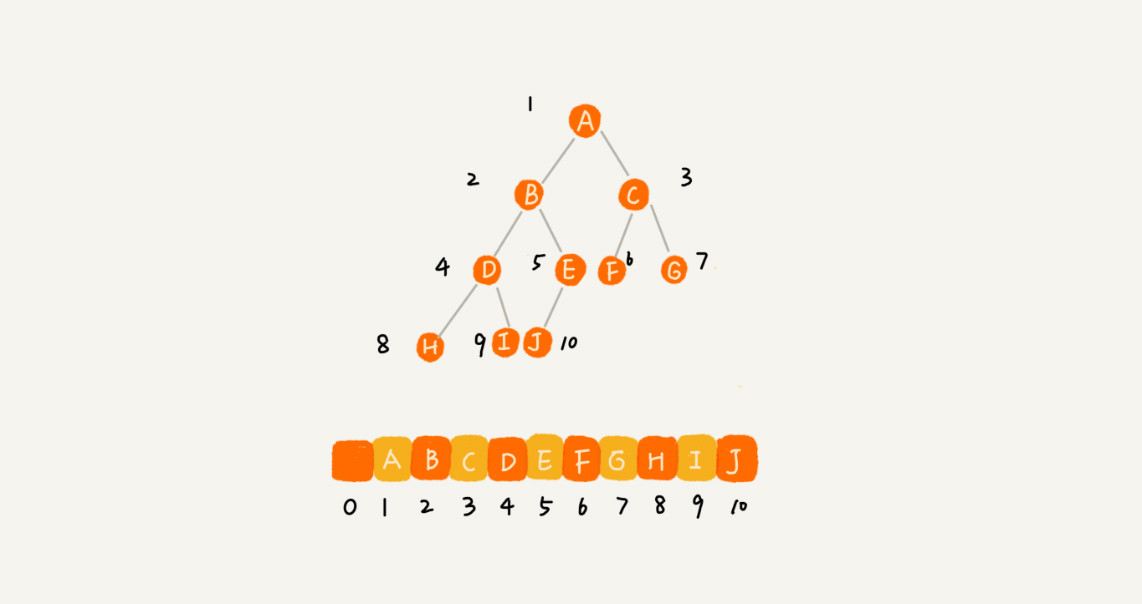我们只要拎住根节点，就可以通过左 右子节点的指针，把整棵树都串起来 2.基于数组的'顺序存储法'把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 * i = 2 的位置， 右子节点存储在 2 * i + 1 = 3 的位置,因此可以得到一个规律：下标为 2 * i 的位置存储的就是左子节点， 下标为 2 * i + 1 的位置存储的就是右子节点。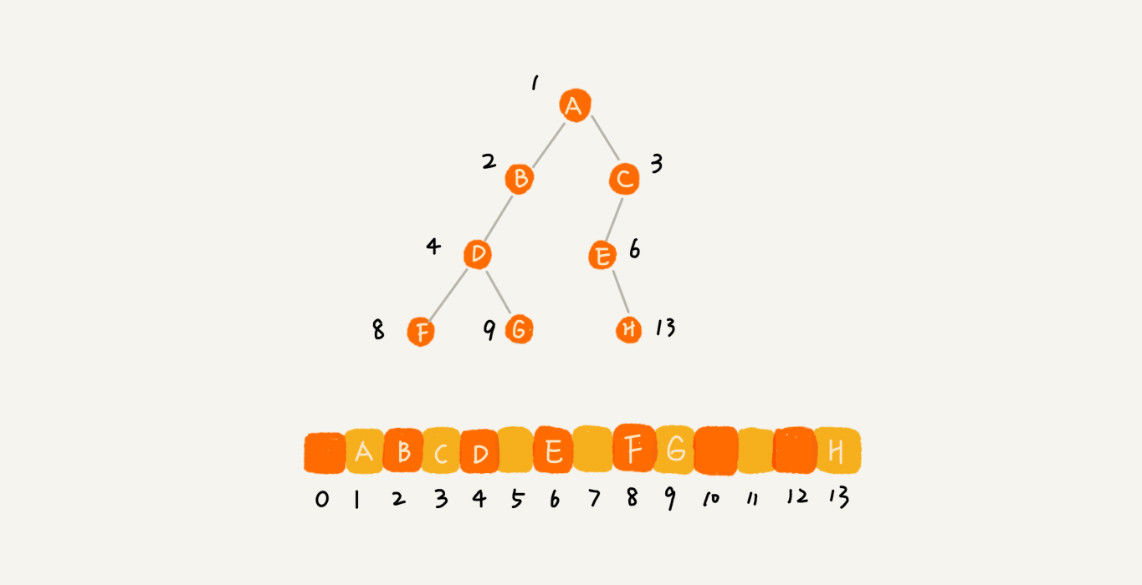反过来，下标为 i/2 的位置存储就是它的父节点 ~~~ * 图片来自数据结构与算法之美 -- 王争老师  * 顺序存储法  * 当顺序存储法遇到不完全二叉树的时候 ~~~ 1.如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。 因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针 2.也是为什么完全二叉树要求最后一层的子节点都靠左的原因。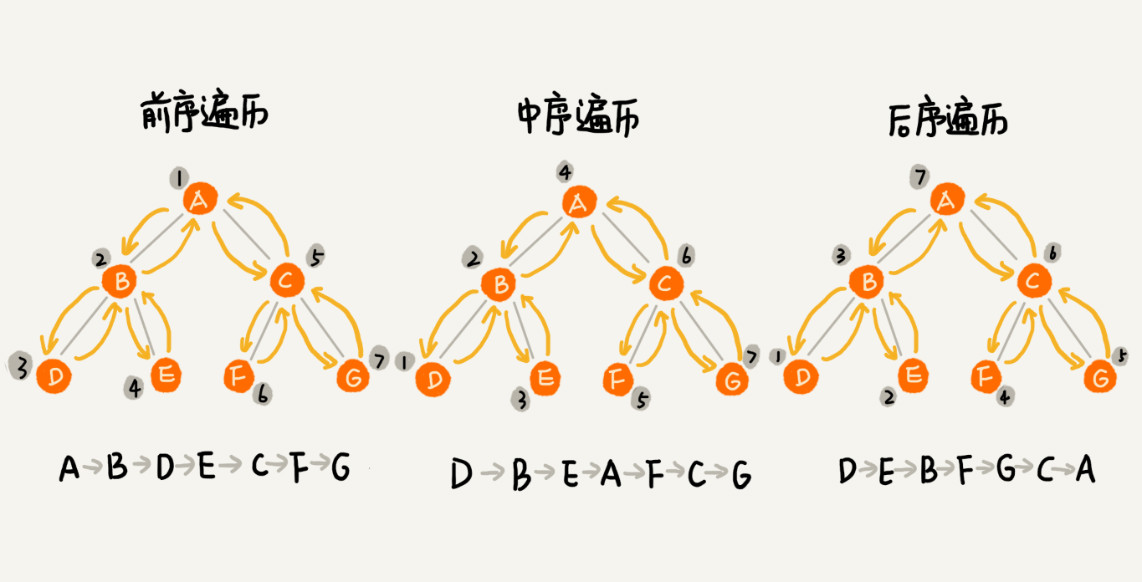 ~~~  >[info] ## 二叉树的遍历 ~~~ 1.经典的方法有三种，'前序遍历'、'中序遍历'和'后序遍历' 2.1.'前序遍历'是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。 2.2.'中序遍历'是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。 2.3.'后序遍历'是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。 2.通过代码实现 void preOrder(Node* root) { // 前 if (root == null) return; print root // 此处为伪代码，表示打印root节点 preOrder(root->left); preOrder(root->right); } void inOrder(Node* root) { // 中 if (root == null) return; inOrder(root->left); print root // 此处为伪代码，表示打印root节点 inOrder(root->right); } void postOrder(Node* root) { // 后 if (root == null) return; postOrder(root->left); postOrder(root->right); print root // 此处为伪代码，表示打印root节点 } ~~~ * 如图