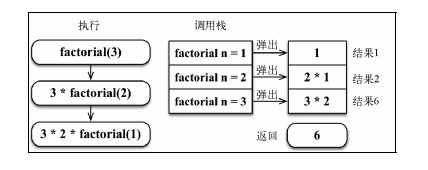
[TOC] js 优化递归使用尾调用优化 >[success] # 递归阶乘 ~~~ 1.求5*4*3*2*1 的问题，用递归来解决三步走 1.1.分解成各个小部分 5 * fn(4) 参数n = 5-1 5 * (4*fn(3)) 参数n = 4-1 5 * 4 * (3*fn(2)) 参数n = 3-1 5 * 4 * 3 * (2*fn(1)) 参数n =2-1 1.2.推到成递归公式 fn(n) = n*fn(n-1) ,且fn(1) = 1 1.3.终止条件 fn(1) = 1 ~~~ >[danger] ##### 代码 ~~~ 1.递归是栈的结构表现，所以它'递'的过程是在做压栈，'归'的过程在做出栈，其实本质，先算的是 终止条件，然后在依次向上传递 2.如图一，通过浏览器的控制台可以更形象的看出这个过程 ~~~ ~~~ // 递归阶乘 求 5*4*3*2*1 // 先拆分 5 * fn(4) 参数n = 5-1 // 5 * (4*fn(3)) 参数n = 4-1 // 5 * 4 * (3*fn(2)) 参数n = 3-1 // 5 * 4 * 3 * (2*fn(1)) 参数n =2-1 // 现在就是一个压栈的过程，从5*fn(4)先进，依次压栈直到最后 fn(1)，执行的时候 // 出栈时候从fn(1) 开始执行，因此为什么要有终止条件也可以理解了 function factorial(n){ console.trace() // 记录堆栈 // 归的过程 -- 墙相当于 乘到了1 if(n===1 || n===0){ return 1 } console.log(n) // 调用 -- 传递的过程 return n * factorial(n-1) } factorial(5) ~~~ * f12 打断点也可发现遵循栈的思路先进后出  * 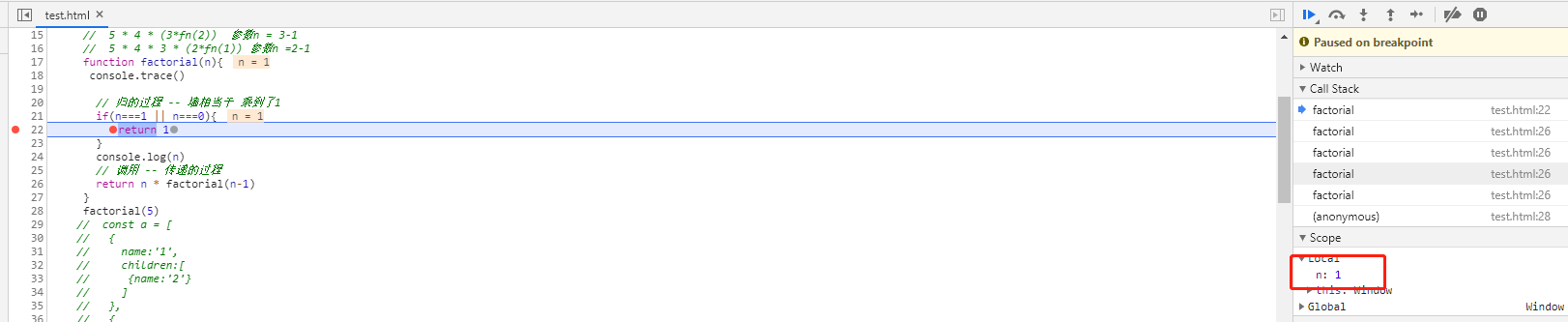运行图解  >[success] # 斐波那契数列 ~~~ 0，1，1，2，3，5，8，13，21 ~~~ >[danger] ##### 不用递归 ~~~ // 斐波那契数列 function fibonacciIterative(n){ if(n < 1) return 0 if(n <=2) return 1 let fib2 = 0 let fib1 = 1 let fibN = 0 for(let i =3;i<=n;i++){ fibN = fib1 + fib2 fib2 = fib1 fib1 = fibN } return fibN } ~~~ >[danger] ##### 使用递归 ~~~ // 斐波那契数列 function fibonacciIterative(n){ if(n < 1) return 0 // 结束条件 if(n <=2) return 1 // 结束条件 return fibonacciIterative(n-2) + fibonacciIterative(n-1) // 递归公式 fn(n) = fn(n-1)+fn(n-2) } ~~~ >[success] # 减少重复递归 -- 记忆化方法 ~~~ 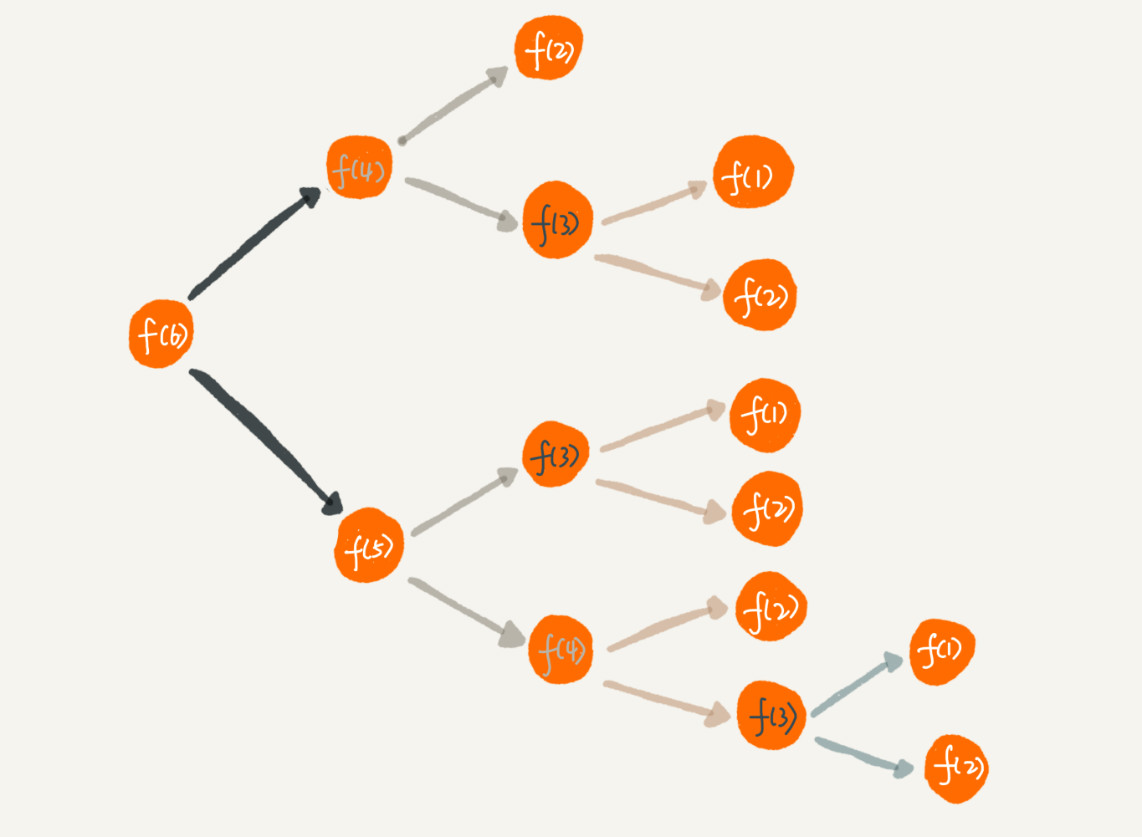1.向求解斐波那契数列时候，将求解过程图形化，可以看出，有些已经 求过的结点我们还会反复在求，如果把这些一求过的数存起来直接用，也会 提高效率 ~~~  >[danger] ##### 代码 ~~~ function fibonacciMemoization(n) { const memo = [0, 1]; const fibonacci = (n) => { if (memo[n] != null) return memo[n]; return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo); }; return fibonacci(n); } ~~~