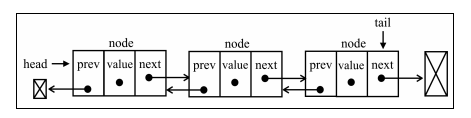
>[success] # 双向链表 ~~~ 1.双向链表相对于单向链表来说'链接是双向的：一个链向下一个元素， 另一个链向前一个元素' 2.就是说双向链表和单链表相比不止有'后继指针next' 它还有一个'前驱指针prev' 3.因为双向链表的结构导致他独有的特性： 3.1.因为有两个指针因此它的没存空间占用会更多，浪费储存空间 3.2.但可以支持双向遍历，这样也带来了双向链表操作的灵活性举个例子： 在单向链表中，如果迭代时错过了要找的元素，就需要回到起点，重新开始迭代。这是双向 链表的一个优势。 4.好处既可以从头查找元素也可以从尾部开始查找元素，可以利用长度/2 来决是头部开始找还是尾部 开始找 ~~~ * 如图 需要每个结点不只有'后继指针next' 它还有一个'前驱指针prev'  >[danger] ##### 代码实现 ~~~ 1.在上面的分析时候，说过链表是非连续的空间，我们需要给'每个节点创建对象',并且这个节点存储的两个东西 '当前节点的值'，'当前节点对应的下一个节点内存指向'，和'上个结点对应的指向'因此根据这两点创建一个类 // 保存Node 节点 指针 我们双向链表只要继承单项链表创建的结点类即可 class Node { constructor(element){ this.element = element this.next = undefined } } 2.可以发现双向链表的节点类，构造函数这里我们传了三个参数，element是必然要有的，剩下两个 不传相当于undefined，前后指针指向为undefined // 双向链表 class DoublyNode extends Node { constructor(element, next, prev) { super(element, next); this.prev = prev; } } // 比较元素的公共方法 function defaultEquals(a, b) { return a === b; } ~~~ ~~~ class DoublyNode extends Node { constructor(element, next, prev) { super(element, next); this.prev = prev; } } // 我们的双向链表可以继承单项链表 // 但在这个 基础上需要稍微的重写内部一些方法 class DoublyLinkedList extends LinkedList { // {4} constructor(equalsFn = defaultEquals) { super(equalsFn); this.tail = undefined; // 双向链表需要 比单向链表多个尾部记录 } // 添加元素 就需要记录两个指针 push(element) { const node = new DoublyNode(element); // 当链表没有元素的时候第一个添加的结点 // 即使尾部也是头部 if (this.head == null) { this.head = node; this.tail = node; } else { this.tail.next = node; // 之前尾部的结点指向当前结点 node.prev = this.tail; // 现在尾部的头部指针指向之前尾部 this.tail = node; // 记录新的尾部结点 } this.count++; } insert(element, index) { if (index >= 0 && index <= this.count) { const node = new DoublyNode(element); let current = this.head; if (index === 0) { // 如果给链表首位插入结点 if (this.head == null) { // 当这个这链表为空的时候 this.head = node; this.tail = node; } else { // 首位插入不为空的时候 node.next = this.head; this.head.prev = node; this.head = node; } } else if (index === this.count) { // 当往尾部插入的时候 current = this.tail; current.next = node; node.prev = current; this.tail = node; } else { // 往其他位置插入元素的时候 const previous = this.getElementAt(index - 1); current = previous.next; node.next = current; previous.next = node; current.prev = node; node.prev = previous; } this.count++; return true; } return false; } // 删除 指定角标元素的时候 removeAt(index) { if (index >= 0 && index < this.count) { let current = this.head; if (index === 0) { // 删除的时候如果是首位 this.head = this.head.next; // 新的头结点为删除的头结点下一结点 if (this.count === 1) { // 如果链表中只有一个元素怎尾部结点为undefined this.tail = undefined; } else { // 当前新的头部结点的前指针就为undefined this.head.prev = undefined; } } else if (index === this.count - 1) { // 尾部结点的时候 current = this.tail; this.tail = current.prev; this.tail.next = undefined; } else { current = this.getElementAt(index); // 找到当前结点 const previous = current.prev; previous.next = current.next; current.next.prev = previous; } this.count--; return current.element; } return undefined; } indexOf(element) { let current = this.head; let index = 0; while (current != null) { if (this.equalsFn(element, current.element)) { return index; } index++; current = current.next; } return -1; } getHead() { return this.head; } getTail() { return this.tail; } clear() { super.clear(); this.tail = undefined; } toString() { if (this.head == null) { return ''; } let objString = `${this.head.element}`; let current = this.head.next; while (current != null) { objString = `${objString},${current.element}`; current = current.next; } return objString; } inverseToString() { if (this.tail == null) { return ''; } let objString = `${this.tail.element}`; let previous = this.tail.prev; while (previous != null) { objString = `${objString},${previous.element}`; previous = previous.prev; } return objString; } } ~~~