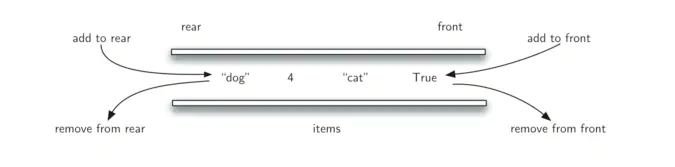
>[success] # 实现一个双端队列 ~~~ 1.双端队列（deque，或称 double-ended queue）是一种允许我们同时从前端和后端添加和移除 元素的特殊队列 2.由于双端队列同时遵守了先进先出和后进先出原则，可以说它是把队列和栈相结合的一种数据结构 ~~~ * 图解  >[danger] ##### 双端队列封装需要的方法 ~~~ 1.addFront(element)：该方法在双端队列前端添加新的元素。 2.addBack(element)：该方法在双端队列后端添加新的元素（实现方法和 Queue 类中的enqueue 方法相同）。 3.removeFront()：该方法会从双端队列前端移除第一个元素（实现方法和 Queue 类中的dequeue 方法相同）。 4.removeBack()：该方法会从双端队列后端移除第一个元素（实现方法和 Stack 类中的pop 方法一样）。 5.peekFront()：该方法返回双端队列前端的第一个元素（实现方法和 Queue 类中的 peek方法一样）。 6.peekBack()：该方法返回双端队列后端的第一个元素（实现方法和 Stack 类中的 peek方法一样）。 ~~~ >[danger] ##### 代码实现 ~~~ // 需要两个标记符号 记录队头 和 队伍尾 // 需要可以有增删改查 class Deque{ constructor(){ this.items = {} this.count = 0 // 记录末尾 this.lowestCount = 0 // 记录头部 } size(){ return this.count - this.lowestCount } isEmpty(){ return this.size === 0 } /* 向头部添加有三种情况 1.当数据为空的时候相当于是在尾部添加 2.当头部数据索引元素大于0时候 正常向头部添加重新记录头部位置 3.当头部数据索引为0的时候就需要移动元素留出0索引 */ addFront(ele){ if(this.isEmpty()){ this.addBack(ele) }else if(this.lowestCount>0){ // 先-- 往当前的lowestCount 标记的前一位加 this.lowestCount -- this.items[this.lowestCount] = ele }else{ // 反向循环 for(let i = this.count;i>0;i--){ this.items[i] = this.items[i-1] } // 移位后要更新新的尾部指针 this.count++ this.items[0] = ele } } // 向末尾添加数据 addBack(ele){ this.items[this.count] = ele this.count ++ } // 移除队伍头部元素 removeFront(){ if(this.isEmpty()){ return undefined } const res = this.items[this.lowestCount] delete this.items[this.lowestCount] this.lowestCount ++ return res } // 移除队伍尾部 removeBack() { if (this.isEmpty()) { return undefined; } this.count--; const result = this.items[this.count]; delete this.items[this.count]; return result; } // 返回头部元素 peekFront() { if (this.isEmpty()) { return undefined; } return this.items[this.lowestCount]; } // 返回尾部元素 peekBack() { if (this.isEmpty()) { return undefined; } return this.items[this.count - 1]; } // 重置 clear() { this.items = {}; this.count = 0; this.lowestCount = 0; } toString() { if (this.isEmpty()) { return ''; } let objString = `${this.items[this.lowestCount]}`; for (let i = this.lowestCount + 1; i < this.count; i++) { objString = `${objString},${this.items[i]}`; } return objString; } } ~~~ * 使用 ~~~ const deque = new Deque(); deque.addBack('John'); deque.addBack('Jack'); deque.removeFront(); deque.removeBack(); deque.addFront('wang'); deque.addFront('wang'); // 打印结果： {0: "wang", 1: "wang"} ~~~ >[info] ## 回文检查 ~~~ 1.利用双端队列首位都可以进出的原则 ~~~ >[danger] ##### 代码 ~~~ export function palindromeChecker(aString) { if ( aString === undefined || aString === null || (aString !== null && aString.length === 0) ) { return false; } const deque = new Deque(); const lowerString = aString.toLocaleLowerCase().split(' ').join(''); let firstChar; let lastChar; for (let i = 0; i < lowerString.length; i++) { deque.addBack(lowerString.charAt(i)); } while (deque.size() > 1) { firstChar = deque.removeFront(); lastChar = deque.removeBack(); if (firstChar !== lastChar) { return false; } } return true; } ~~~ * 运行 下面打印都为true ~~~ console.log('a', palindromeChecker('a')); console.log('aa', palindromeChecker('aa')); console.log('kayak', palindromeChecker('kayak')); console.log('level', palindromeChecker('level')); console.log('Was it a car or a cat I saw', palindromeChecker('Was it a car or a cat I saw')); console.log('Step on no pets', palindromeChecker('Step on no pets')); ~~~ >[danger] ##### 总结 ~~~ 1.也可以用已知的api 来做这道题 ~~~ ~~~ var isPalindrome = function(x) { if ( x < 0 ) return false let str = '' + x // 转成字符串类型 return Array.from(str).reverse().join('') === str }; ~~~