## 背景
在物联网、监控、传感器、金融等应用领域,数据在时间维度上流式的产生,而且数据量非常庞大。
例如我们经常看到的性能监控视图,就是很多点在时间维度上描绘的曲线。
又比如金融行业的走势数据等等。
我们想象一下,如果每个传感器或指标每100毫秒产生1个点,一天就是864000个点。
而传感器或指标是非常多的,例如有100万个传感器或指标,一天的量就接近一亿的量。
假设我们要描绘一个时间段的图形,这么多的点,渲染估计都要很久。
那么有没有好的压缩算法,即能保证失真度,又能很好的对数据进行压缩呢?
## 旋转门压缩算法原理
旋转门压缩算法(SDT)是一种直线趋势化压缩算法,其本质是通过一条由起点和终点确定的直线代替一系列连续数据点。
该算法需要记录每段时间间隔长度、起点数据和终点数据, 前一段的终点数据即为下一段的起点数据。
其基本原理较为简单, 参见图。
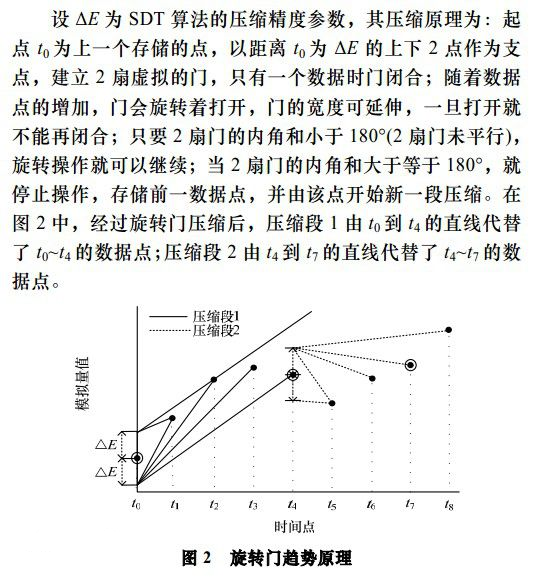
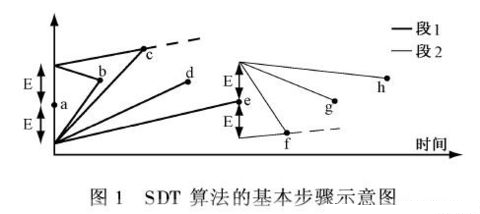
第一个数据点a上下各有一点,它们与a点之间的距离为E(即门的宽度), 这两个点作为“门”的两个支点。
当只有第一个数据点时,两扇门都是关闭的;随着点数越来越多,门将逐步打开;注意到每扇门的宽度是可以伸缩的,在一段时间间隔里面,门一旦打开就不能闭;
只要两扇门未达到平行,或者说两个内角之和小于180°(本文的算法将利用这一点进行判断),这种“转门”操作即可继续进行。
图中第一个时间段是从a到e, 结果是用a点到e点之间的直线代替数据点(a,b,c,d,e); 起到了可控失真(E)的压缩作用。
第二个时间间隔从e点开始,开始时两扇门关闭,然后逐步打开,后续操作与前一段类似。
## 在PostgreSQL中实现旋转门压缩算法
通过旋转门算法的原理,可以了解到,有几个必要的输入项。
* 有x坐标和y坐标的点(如果是时间轴上的点,可以通过epoch转换成这种形式)
* E,即门的宽度,起到了控制压缩失真度的作用
### 例子
#### 创建测试表
~~~
create table tbl(id int, -- ID,可有可无
val numeric, -- 值(如传感器或金融行业的点值)
t timestamp -- 取值时间戳
);
~~~
#### 插入10万条测试数据
~~~
insert into tbl select generate_series(1,100000), round((random()*100)::numeric, 2), clock_timestamp()+(generate_series(1,100000) || ' second')::interval ;
test=> select * from tbl limit 10;
id | val | t
----+-------+----------------------------
1 | 31.79 | 2016-08-12 23:22:27.530318
2 | 18.23 | 2016-08-12 23:22:28.530443
3 | 5.14 | 2016-08-12 23:22:29.530453
4 | 90.25 | 2016-08-12 23:22:30.530459
5 | 8.17 | 2016-08-12 23:22:31.530465
6 | 97.43 | 2016-08-12 23:22:32.53047
7 | 17.41 | 2016-08-12 23:22:33.530476
8 | 0.23 | 2016-08-12 23:22:34.530481
9 | 84.67 | 2016-08-12 23:22:35.530487
10 | 16.37 | 2016-08-12 23:22:36.530493
(10 rows)
~~~
#### 时间如何转换成X轴的数值,假设每1秒为X坐标的1个单位
~~~
test=> select (extract(epoch from t)-extract(epoch from first_value(t) over())) / 1 as x, -- 除以1秒为1个单位
val, t from tbl limit 100;
x | val | t
------------------+-------+----------------------------
0 | 31.79 | 2016-08-12 23:22:27.530318
1.00012493133545 | 18.23 | 2016-08-12 23:22:28.530443
2.00013494491577 | 5.14 | 2016-08-12 23:22:29.530453
3.00014090538025 | 90.25 | 2016-08-12 23:22:30.530459
4.00014686584473 | 8.17 | 2016-08-12 23:22:31.530465
5.00015187263489 | 97.43 | 2016-08-12 23:22:32.53047
6.00015807151794 | 17.41 | 2016-08-12 23:22:33.530476
7.00016307830811 | 0.23 | 2016-08-12 23:22:34.530481
8.00016903877258 | 84.67 | 2016-08-12 23:22:35.530487
~~~
#### 编写实现螺旋门算法的函数
~~~
create or replace function f (
i_radius numeric, -- 压缩半径
i_time timestamp, -- 开始时间
i_interval_s numeric, -- 时间转换间隔 (秒,例如每5秒在坐标上表示1个单位间隔,则这里使用5)
OUT o_val numeric, -- 值,纵坐标 y (跳跃点y)
OUT o_time timestamp, -- 时间,横坐标 x (跳跃点x)
OUT o_x numeric -- 跳跃点x, 通过 o_time 转换
)
returns setof record as $$
declare
v_time timestamp; -- 时间变量
v_x numeric; -- v_time 转换为v_x
v_val numeric; -- y坐标
v1_time timestamp; -- 前一点 时间变量
v1_x numeric; -- 前一点 v_time 转换为v_x
v1_val numeric; -- 前一点 y坐标
v_start_time numeric; -- 记录第一条的时间坐标, 用于计算x偏移量
v_rownum int8; -- 用于标记是否第一行
v_max_angle1 numeric; -- 最大上门夹角角度
v_max_angle2 numeric; -- 最大下门夹角角度
v_angle1 numeric; -- 上门夹角角度
v_angle2 numeric; -- 下门夹角角度
begin
for v_rownum, v_time , v_val in select row_number() over(), t, val from tbl where t>i_time order by t limit 100 -- 这条QUERY可以做成execute的动态QUERY,本文略
LOOP
-- 第一行,第一个点,是实际要记录的点位
if v_rownum=1 then
v_start_time := extract(epoch from v_time);
v_x := 0;
o_val := v_val;
o_time := v_time;
o_x := v_x;
-- raise notice 'rownum=1 %, %', o_val,o_time;
return next; -- 返回第一个点
else
v_x := (extract(epoch from v_time) - v_start_time) / i_interval_s; -- 生成X坐标
SELECT 180-ST_Azimuth(
ST_MakePoint(o_x, o_val+i_radius), -- 门上点
ST_MakePoint(v_x, v_val) -- next point
)/(2*pi())*360 as degAz, -- 上夹角
ST_Azimuth(
ST_MakePoint(o_x, o_val-i_radius), -- 门下点
ST_MakePoint(v_x, v_val) -- next point
)/(2*pi())*360 As degAzrev -- 下夹角
INTO v_angle1, v_angle2;
select GREATEST(v_angle1, v_max_angle1), GREATEST(v_angle2, v_max_angle2) into v_max_angle1, v_max_angle2;
if (v_max_angle1 + v_max_angle2) >= 180 then -- 找到四边形外的点位,输出上一个点,并从上一个点开始重新计算四边形
-- raise notice 'max1 %, max2 %', v_max_angle1 , v_max_angle2;
-- 复原
v_angle1 := 0;
v_max_angle1 := 0;
v_angle2 := 0;
v_max_angle2 := 0;
-- 门已完全打开,输出前一个点的值
o_val := v1_val;
o_time := v1_time;
v1_x := (extract(epoch from v1_time) - v_start_time) / i_interval_s; -- 生成前一个点的X坐标
o_x := v1_x;
-- 用新的门,与当前点计算新的夹角
SELECT 180-ST_Azimuth(
ST_MakePoint(o_x, o_val+i_radius), -- 门上点
ST_MakePoint(v_x, v_val) -- next point
)/(2*pi())*360 as degAz, -- 上夹角
ST_Azimuth(
ST_MakePoint(o_x, o_val-i_radius), -- 门下点
ST_MakePoint(v_x, v_val) -- next point
)/(2*pi())*360 As degAzrev -- 下夹角
INTO v_angle1, v_angle2;
select GREATEST(v_angle1, v_max_angle1), GREATEST(v_angle2, v_max_angle2) into v_max_angle1, v_max_angle2;
-- raise notice 'new max %, new max %', v_max_angle1 , v_max_angle2;
-- raise notice 'rownum<>1 %, %', o_val, o_time;
return next;
end if;
-- 记录当前值,保存作为下一个点的前点
v1_val := v_val;
v1_time := v_time;
end if;
END LOOP;
end;
$$ language plpgsql strict;
~~~
#### 压缩测试
门宽为15,起始时间为’2016-08-12 23:22:27.530318’,每1秒表示1个X坐标单位。
~~~
test=> select * from f(15,'2016-08-12 23:22:27.530318',1);
o_val | o_time | o_x
-------+----------------------------+------------------
18.23 | 2016-08-12 23:22:28.530443 | 0
5.14 | 2016-08-12 23:22:29.530453 | 1.00001287460327
90.25 | 2016-08-12 23:22:30.530459 | 2.00001883506775
......
87.90 | 2016-08-12 23:24:01.53098 | 93.0005400180817
29.94 | 2016-08-12 23:24:02.530985 | 94.0005450248718
63.53 | 2016-08-12 23:24:03.53099 | 95.0005497932434
12.25 | 2016-08-12 23:24:04.530996 | 96.0005559921265
83.21 | 2016-08-12 23:24:05.531001 | 97.0005609989166
(71 rows)
~~~
可以看到100个点,压缩成了71个点。
#### 对比一下原来的100个点的值
~~~
test=> select val, t, (extract(epoch from t)-extract(epoch from first_value(t) over()))/1 as x from tbl where t>'2016-08-12 23:22:27.530318' order by t limit 100;
val | t | x
-------+----------------------------+------------------
18.23 | 2016-08-12 23:22:28.530443 | 0
5.14 | 2016-08-12 23:22:29.530453 | 1.00001001358032
90.25 | 2016-08-12 23:22:30.530459 | 2.0000159740448
......
83.21 | 2016-08-12 23:24:05.531001 | 97.0005581378937
87.97 | 2016-08-12 23:24:06.531006 | 98.0005631446838
58.97 | 2016-08-12 23:24:07.531012 | 99.0005691051483
(100 rows)
~~~
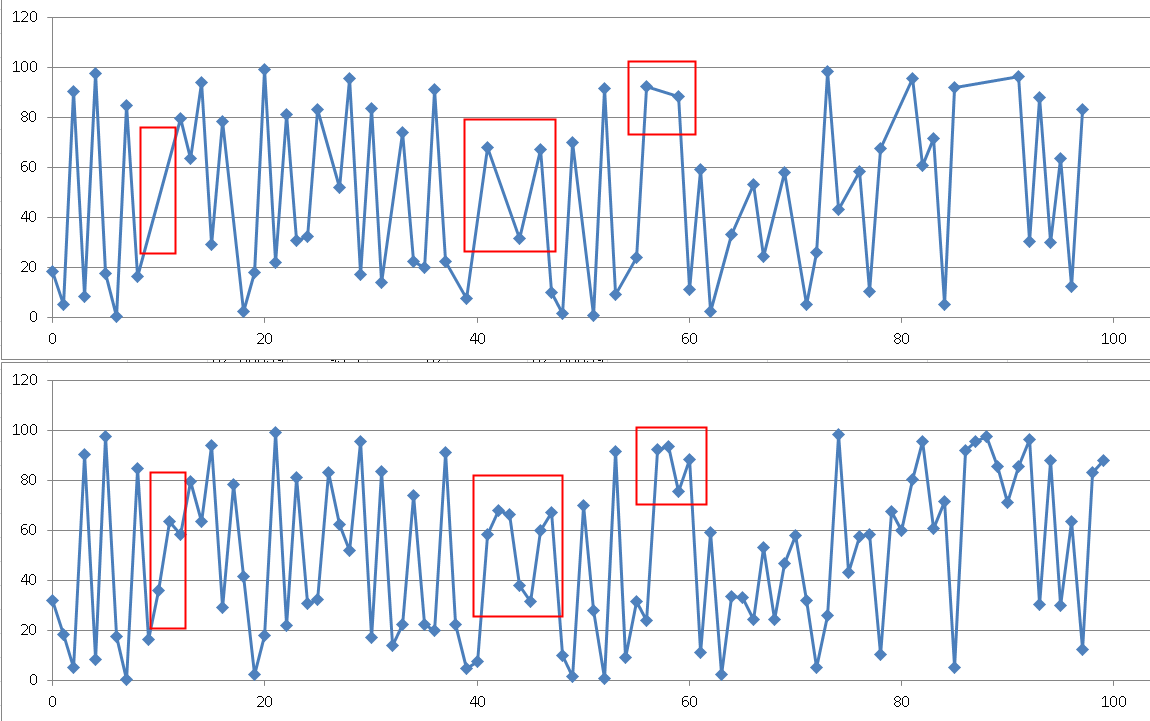
使用excel绘图,进行压缩前后的对比
上面是压缩后的数据绘图,下面是压缩前的数据绘图
红色标记的位置,就是通过旋转门算法压缩掉的数据。
失真度是可控的。
## 流式压缩的实现
本文略,其实也很简单,这个函数改一下,创建一个以数组为输入参数的函数。
以lambda的方式,实时的从流式输入的管道取数,并执行即可。
也可以写成聚合函数,在基于PostgreSQL 的流式数据库pipelineDB中调用,实现流式计算。
## 小结
通过旋转门算法,对IT监控、金融、电力、水利等监控、物联网、等流式数据进行实时的压缩。
数据不需要从数据库LOAD出来即可在库内完成运算和压缩。
用户也可以根据实际的需求,进行流式的数据压缩,同样数据也不需要从数据库LOAD出来,在数据库端即可完成。
PostgreSQL的功能一如既往的强大,好用,快用起来吧。
## 参考
1. http://baike.baidu.com/view/3478397.htm
2. http://postgis.net/docs/manual-2.2/ST_Azimuth.html
3. https://www.postgresql.org/docs/devel/static/functions-conditional.html
4. http://gis.stackexchange.com/questions/25126/how-to-calculate-the-angle-at-which-two-lines-intersect-in-postgis
5. http://gis.stackexchange.com/questions/668/how-can-i-calculate-the-bearing-between-two-points-in-postgis
6. http://www.pipelinedb.com/
- 数据库内核月报目录
- 数据库内核月报 - 2016/09
- MySQL · 社区贡献 · AliSQL那些事儿
- PetaData · 架构体系 · PetaData第二代低成本存储体系
- MySQL · 社区动态 · MariaDB 10.2 前瞻
- MySQL · 特性分析 · 执行计划缓存设计与实现
- PgSQL · 最佳实践 · pg_rman源码浅析与使用
- MySQL · 捉虫状态 · bug分析两例
- PgSQL · 源码分析 · PG优化器浅析
- MongoDB · 特性分析· Sharding原理与应用
- PgSQL · 源码分析 · PG中的无锁算法和原子操作应用一则
- SQLServer · 最佳实践 · TEMPDB的设计
- 数据库内核月报 - 2016/08
- MySQL · 特性分析 ·MySQL 5.7新特性系列四
- PgSQL · PostgreSQL 逻辑流复制技术的秘密
- MySQL · 特性分析 · MyRocks简介
- GPDB · 特性分析· Greenplum 备份架构
- SQLServer · 最佳实践 · RDS for SQLServer 2012权限限制提升与改善
- TokuDB · 引擎特性 · REPLACE 语句优化
- MySQL · 专家投稿 · InnoDB物理行中null值的存储的推断与验证
- PgSQL · 实战经验 · 旋转门压缩算法在PostgreSQL中的实现
- MySQL · 源码分析 · Query Cache并发处理
- PgSQL · 源码分析· pg_dump分析
- 数据库内核月报 - 2016/07
- MySQL · 特性分析 ·MySQL 5.7新特性系列三
- MySQL · 特性分析 · 5.7 代价模型浅析
- PgSQL · 实战经验 · 分组TOP性能提升44倍
- MySQL · 源码分析 · 网络通信模块浅析
- MongoDB · 特性分析 · 索引原理
- SQLServer · 特性分析 · XML与JSON应用比较
- MySQL · 最佳实战 · 审计日志实用案例分析
- MySQL · 性能优化 · 条件下推到物化表
- MySQL · 源码分析 · Query Cache内部剖析
- MySQL · 捉虫动态 · 备库1206错误问题说明
- 数据库内核月报 - 2016/06
- MySQL · 特性分析 · innodb 锁分裂继承与迁移
- MySQL · 特性分析 ·MySQL 5.7新特性系列二
- PgSQL · 实战经验 · 如何预测Freeze IO风暴
- GPDB · 特性分析· Filespace和Tablespace
- MariaDB · 新特性 · 窗口函数
- MySQL · TokuDB · checkpoint过程
- MySQL · 特性分析 · 内部临时表
- MySQL · 最佳实践 · 空间优化
- SQLServer · 最佳实践 · 数据库实现大容量插入的几种方式
- 数据库内核月报 - 2016/05
- MySQL · 引擎特性 · 基于InnoDB的物理复制实现
- MySQL · 特性分析 · MySQL 5.7新特性系列一
- PostgreSQL · 特性分析 · 逻辑结构和权限体系
- MySQL · 特性分析 · innodb buffer pool相关特性
- PG&GP · 特性分析 · 外部数据导入接口实现分析
- SQLServer · 最佳实践 · 透明数据加密在SQLServer的应用
- MySQL · TokuDB · 日志子系统和崩溃恢复过程
- MongoDB · 特性分析 · Sharded cluster架构原理
- PostgreSQL · 特性分析 · 统计信息计算方法
- MySQL · 捉虫动态 · left-join多表导致crash
- 数据库内核月报 - 2016/04
- MySQL · 参数故事 · innodb_additional_mem_pool_size
- GPDB · 特性分析 · Segment事务一致性与异常处理
- GPDB · 特性分析 · Segment 修复指南
- MySQL · 捉虫动态 · 并行复制外键约束问题二
- PgSQL · 性能优化 · 如何潇洒的处理每天上百TB的数据增量
- Memcached · 最佳实践 · 热点 Key 问题解决方案
- MongoDB · 最佳实践 · 短连接Auth性能优化
- MySQL · 最佳实践 · RDS 只读实例延迟分析
- MySQL · TokuDB · TokuDB索引结构--Fractal Tree
- MySQL · TokuDB · Savepoint漫谈
- 数据库内核月报 - 2016/03
- MySQL · TokuDB · 事务子系统和 MVCC 实现
- MongoDB · 特性分析 · MMAPv1 存储引擎原理
- PgSQL · 源码分析 · 优化器逻辑推理
- SQLServer · BUG分析 · Agent 链接泄露分析
- Redis · 特性分析 · AOF Rewrite 分析
- MySQL · BUG分析 · Rename table 死锁分析
- MySQL · 物理备份 · Percona XtraBackup 备份原理
- GPDB · 特性分析· GreenPlum FTS 机制
- MySQL · 答疑解惑 · 备库Seconds_Behind_Master计算
- MySQL · 答疑解惑 · MySQL 锁问题最佳实践
- 数据库内核月报 - 2016/02
- MySQL · 引擎特性 · InnoDB 文件系统之文件物理结构
- MySQL · 引擎特性 · InnoDB 文件系统之IO系统和内存管理
- MySQL · 特性分析 · InnoDB transaction history
- PgSQL · 会议见闻 · PgConf.Russia 2016 大会总结
- PgSQL · 答疑解惑 · PostgreSQL 9.6 并行查询实现分析
- MySQL · TokuDB · TokuDB之黑科技工具
- PgSQL · 性能优化 · PostgreSQL TPC-C极限优化玩法
- MariaDB · 版本特性 · MariaDB 的 GTID 介绍
- MySQL · 特性分析 · 线程池
- MySQL · 答疑解惑 · mysqldump tips 两则
- 数据库内核月报 - 2016/01
- MySQL · 引擎特性 · InnoDB 事务锁系统简介
- GPDB · 特性分析· GreenPlum Primary/Mirror 同步机制
- MySQL · 专家投稿 · MySQL5.7 的 JSON 实现
- MySQL · 特性分析 · 优化器 MRR & BKA
- MySQL · 答疑解惑 · 物理备份死锁分析
- MySQL · TokuDB · Cachetable 的工作线程和线程池
- MySQL · 特性分析 · drop table的优化
- MySQL · 答疑解惑 · GTID不一致分析
- PgSQL · 特性分析 · Plan Hint
- MariaDB · 社区动态 · MariaDB on Power8 (下)
- 数据库内核月报 - 2015/12
- MySQL · 引擎特性 · InnoDB 事务子系统介绍
- PgSQL · 特性介绍 · 全文搜索介绍
- MongoDB · 捉虫动态 · Kill Hang问题排查记录
- MySQL · 参数优化 ·RDS MySQL参数调优最佳实践
- PgSQL · 特性分析 · 备库激活过程分析
- MySQL · TokuDB · 让Hot Backup更完美
- PgSQL · 答疑解惑 · 表膨胀
- MySQL · 特性分析 · Index Condition Pushdown (ICP)
- MariaDB · 社区动态 · MariaDB on Power8
- MySQL · 特性分析 · 企业版特性一览
- 数据库内核月报 - 2015/11
- MySQL · 社区见闻 · OOW 2015 总结 MySQL 篇
- MySQL · 特性分析 · Statement Digest
- PgSQL · 答疑解惑 · PostgreSQL 用户组权限管理
- MySQL · 特性分析 · MDL 实现分析
- PgSQL · 特性分析 · full page write 机制
- MySQL · 捉虫动态 · MySQL 外键异常分析
- MySQL · 答疑解惑 · MySQL 优化器 range 的代价计算
- MySQL · 捉虫动态 · ORDER/GROUP BY 导致 mysqld crash
- MySQL · TokuDB · TokuDB 中的行锁
- MySQL · 捉虫动态 · order by limit 造成优化器选择索引错误
- 数据库内核月报 - 2015/10
- MySQL · 引擎特性 · InnoDB 全文索引简介
- MySQL · 特性分析 · 跟踪Metadata lock
- MySQL · 答疑解惑 · 索引过滤性太差引起CPU飙高分析
- PgSQL · 特性分析 · PG主备流复制机制
- MySQL · 捉虫动态 · start slave crash 诊断分析
- MySQL · 捉虫动态 · 删除索引导致表无法打开
- PgSQL · 特性分析 · PostgreSQL Aurora方案与DEMO
- TokuDB · 捉虫动态 · CREATE DATABASE 导致crash问题
- PgSQL · 特性分析 · pg_receivexlog工具解析
- MySQL · 特性分析 · MySQL权限存储与管理
- 数据库内核月报 - 2015/09
- MySQL · 引擎特性 · InnoDB Adaptive hash index介绍
- PgSQL · 特性分析 · clog异步提交一致性、原子操作与fsync
- MySQL · 捉虫动态 · BUG 几例
- PgSQL · 答疑解惑 · 诡异的函数返回值
- MySQL · 捉虫动态 · 建表过程中crash造成重建表失败
- PgSQL · 特性分析 · 谈谈checkpoint的调度
- MySQL · 特性分析 · 5.6 并行复制恢复实现
- MySQL · 备库优化 · relay fetch 备库优化
- MySQL · 特性分析 · 5.6并行复制事件分发机制
- MySQL · TokuDB · 文件目录谈
- 数据库内核月报 - 2015/08
- MySQL · 社区动态 · InnoDB Page Compression
- PgSQL · 答疑解惑 · RDS中的PostgreSQL备库延迟原因分析
- MySQL · 社区动态 · MySQL5.6.26 Release Note解读
- PgSQL · 捉虫动态 · 执行大SQL语句提示无效的内存申请大小
- MySQL · 社区动态 · MariaDB InnoDB表空间碎片整理
- PgSQL · 答疑解惑 · 归档进程cp命令的core文件追查
- MySQL · 答疑解惑 · open file limits
- MySQL · TokuDB · 疯狂的 filenum++
- MySQL · 功能分析 · 5.6 并行复制实现分析
- MySQL · 功能分析 · MySQL表定义缓存
- 数据库内核月报 - 2015/07
- MySQL · 引擎特性 · Innodb change buffer介绍
- MySQL · TokuDB · TokuDB Checkpoint机制
- PgSQL · 特性分析 · 时间线解析
- PgSQL · 功能分析 · PostGIS 在 O2O应用中的优势
- MySQL · 引擎特性 · InnoDB index lock前世今生
- MySQL · 社区动态 · MySQL内存分配支持NUMA
- MySQL · 答疑解惑 · 外键删除bug分析
- MySQL · 引擎特性 · MySQL logical read-ahead
- MySQL · 功能介绍 · binlog拉取速度的控制
- MySQL · 答疑解惑 · 浮点型的显示问题
- 数据库内核月报 - 2015/06
- MySQL · 引擎特性 · InnoDB 崩溃恢复过程
- MySQL · 捉虫动态 · 唯一键约束失效
- MySQL · 捉虫动态 · ALTER IGNORE TABLE导致主备不一致
- MySQL · 答疑解惑 · MySQL Sort 分页
- MySQL · 答疑解惑 · binlog event 中的 error code
- PgSQL · 功能分析 · Listen/Notify 功能
- MySQL · 捉虫动态 · 任性的 normal shutdown
- PgSQL · 追根究底 · WAL日志空间的意外增长
- MySQL · 社区动态 · MariaDB Role 体系
- MySQL · TokuDB · TokuDB数据文件大小计算
- 数据库内核月报 - 2015/05
- MySQL · 引擎特性 · InnoDB redo log漫游
- MySQL · 专家投稿 · MySQL数据库SYS CPU高的可能性分析
- MySQL · 捉虫动态 · 5.6 与 5.5 InnoDB 不兼容导致 crash
- MySQL · 答疑解惑 · InnoDB 预读 VS Oracle 多块读
- PgSQL · 社区动态 · 9.5 新功能BRIN索引
- MySQL · 捉虫动态 · MySQL DDL BUG
- MySQL · 答疑解惑 · set names 都做了什么
- MySQL · 捉虫动态 · 临时表操作导致主备不一致
- TokuDB · 引擎特性 · zstd压缩算法
- MySQL · 答疑解惑 · binlog 位点刷新策略
- 数据库内核月报 - 2015/04
- MySQL · 引擎特性 · InnoDB undo log 漫游
- TokuDB · 产品新闻 · RDS TokuDB小手册
- PgSQL · 社区动态 · 说一说PgSQL 9.4.1中的那些安全补丁
- MySQL · 捉虫动态 · 连接断开导致XA事务丢失
- MySQL · 捉虫动态 · GTID下slave_net_timeout值太小问题
- MySQL · 捉虫动态 · Relay log 中 GTID group 完整性检测
- MySQL · 答疑释惑 · UPDATE交换列单表和多表的区别
- MySQL · 捉虫动态 · 删被引用索引导致crash
- MySQL · 答疑释惑 · GTID下auto_position=0时数据不一致
- 数据库内核月报 - 2015/03
- MySQL · 答疑释惑· 并发Replace into导致的死锁分析
- MySQL · 性能优化· 5.7.6 InnoDB page flush 优化
- MySQL · 捉虫动态· pid file丢失问题分析
- MySQL · 答疑释惑· using filesort VS using temporary
- MySQL · 优化限制· MySQL index_condition_pushdown
- MySQL · 捉虫动态·DROP DATABASE外键约束的GTID BUG
- MySQL · 答疑释惑· lower_case_table_names 使用问题
- PgSQL · 特性分析· Logical Decoding探索
- PgSQL · 特性分析· jsonb类型解析
- TokuDB ·引擎机制· TokuDB线程池
- 数据库内核月报 - 2015/02
- MySQL · 性能优化· InnoDB buffer pool flush策略漫谈
- MySQL · 社区动态· 5.6.23 InnoDB相关Bugfix
- PgSQL · 特性分析· Replication Slot
- PgSQL · 特性分析· pg_prewarm
- MySQL · 答疑释惑· InnoDB丢失自增值
- MySQL · 答疑释惑· 5.5 和 5.6 时间类型兼容问题
- MySQL · 捉虫动态· 变量修改导致binlog错误
- MariaDB · 特性分析· 表/表空间加密
- MariaDB · 特性分析· Per-query variables
- TokuDB · 特性分析· 日志详解
- 数据库内核月报 - 2015/01
- MySQL · 性能优化· Group Commit优化
- MySQL · 新增特性· DDL fast fail
- MySQL · 性能优化· 启用GTID场景的性能问题及优化
- MySQL · 捉虫动态· InnoDB自增列重复值问题
- MySQL · 优化改进· 复制性能改进过程
- MySQL · 谈古论今· key分区算法演变分析
- MySQL · 捉虫动态· mysql client crash一例
- MySQL · 捉虫动态· 设置 gtid_purged 破坏AUTO_POSITION复制协议
- MySQL · 捉虫动态· replicate filter 和 GTID 一起使用的问题
- TokuDB·特性分析· Optimize Table
- 数据库内核月报 - 2014/12
- MySQL· 性能优化·5.7 Innodb事务系统
- MySQL· 踩过的坑·5.6 GTID 和存储引擎那会事
- MySQL· 性能优化·thread pool 原理分析
- MySQL· 性能优化·并行复制外建约束问题
- MySQL· 答疑释惑·binlog event有序性
- MySQL· 答疑释惑·server_id为0的Rotate
- MySQL· 性能优化·Bulk Load for CREATE INDEX
- MySQL· 捉虫动态·Opened tables block read only
- MySQL· 优化改进· GTID启动优化
- TokuDB· Binary Log Group Commit with TokuDB
- 数据库内核月报 - 2014/11
- MySQL· 捉虫动态·OPTIMIZE 不存在的表
- MySQL· 捉虫动态·SIGHUP 导致 binlog 写错
- MySQL· 5.7改进·Recovery改进
- MySQL· 5.7特性·高可用支持
- MySQL· 5.7优化·Metadata Lock子系统的优化
- MySQL· 5.7特性·在线Truncate undo log 表空间
- MySQL· 性能优化·hash_scan 算法的实现解析
- TokuDB· 版本优化· 7.5.0
- TokuDB· 引擎特性· FAST UPDATES
- MariaDB· 性能优化·filesort with small LIMIT optimization
- 数据库内核月报 - 2014/10
- MySQL· 5.7重构·Optimizer Cost Model
- MySQL· 系统限制·text字段数
- MySQL· 捉虫动态·binlog重放失败
- MySQL· 捉虫动态·从库OOM
- MySQL· 捉虫动态·崩溃恢复失败
- MySQL· 功能改进·InnoDB Warmup特性
- MySQL· 文件结构·告别frm文件
- MariaDB· 新鲜特性·ANALYZE statement 语法
- TokuDB· 主备复制·Read Free Replication
- TokuDB· 引擎特性·压缩
- 数据库内核月报 - 2014/09
- MySQL· 捉虫动态·GTID 和 DELAYED
- MySQL· 限制改进·GTID和升级
- MySQL· 捉虫动态·GTID 和 binlog_checksum
- MySQL· 引擎差异·create_time in status
- MySQL· 参数故事·thread_concurrency
- MySQL· 捉虫动态·auto_increment
- MariaDB· 性能优化·Extended Keys
- MariaDB·主备复制·CREATE OR REPLACE
- TokuDB· 参数故事·数据安全和性能
- TokuDB· HA方案·TokuDB热备
- 数据库内核月报 - 2014/08
- MySQL· 参数故事·timed_mutexes
- MySQL· 参数故事·innodb_flush_log_at_trx_commit
- MySQL· 捉虫动态·Count(Distinct) ERROR
- MySQL· 捉虫动态·mysqldump BUFFER OVERFLOW
- MySQL· 捉虫动态·long semaphore waits
- MariaDB·分支特性·支持大于16K的InnoDB Page Size
- MariaDB·分支特性·FusionIO特性支持
- TokuDB· 性能优化·Bulk Fetch
- TokuDB· 数据结构·Fractal-Trees与LSM-Trees对比
- TokuDB·社区八卦·TokuDB团队
