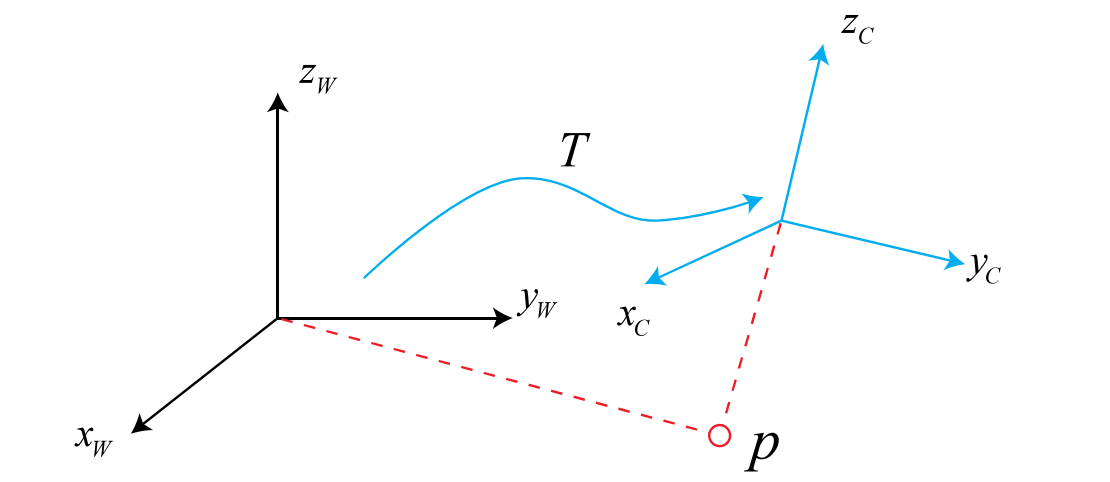
# 附录1 三维空间刚体运动 ## 旋转矩阵 $$\quad$$在机器人运动的过程当中，我们通常会设定一个惯性坐标系（或者叫世界坐标系），姑且认为这个坐标系是固定不动的。例如：$$X_W,Y_W,Z_W$$是固定不动的世界坐标系，$$X_C,Y_C,Z_C$$是机器人坐标系。存在一个向量$$P$$，在世界坐标系下的坐标是$$P_W$$，在移动机器人坐标系下的坐标是$$P_C$$，通常情况下，我们通过传感器已知移动机器人坐标系统下的坐标$$P_C$$，来求$$P$$在世界坐标系下的坐标$$P_W$$  $$\quad$$为了求$$P_W$$，我们必须知道机器人坐标系$$X_C,Y_C,Z_C$$相对与世界坐标$$X_W,Y_W,Z_W$$做了哪些变换。我们定义世界坐标系经过变换矩阵$$T$$之后得到机器人坐标系（这可以通过计算里程和IMU的数据进行测量出来）（这也就说明了为什么在机器人刚刚启动的时候odom和base\_link坐标系必须是重合的，不然没有办法计算旋转矩阵），另外一般情况下，移动机器人运动是一个刚体运动，也就是说机器人的形状和大小不会因为坐标系不同而改变，这种变换叫做欧式变换。一个欧式变换可以由旋转和平移两个部分组成。首先我们考虑旋转问题，假设在世界坐标系下的单位正交基$$(e_x,e_y,e_z)$$，在移动机器人坐标系下的单位正交基$$(e^"_x,e^"_y,e^"_z)$$,那么，根据向量$$P$$的模可知： $$ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad [e_x,e_y,e_z] \cdot P^T_W=[e^"_x,e^"_y,e^"_z] \cdot P^T_C $$ $$\quad$$因此，$$P^T_C=[e_x,e_y,e_z]^T \cdot [e^"_x,e^"_y,e^"_z] \cdot P^T_W$$，我们将$$[e_x,e_y,e_z]^T \cdot [e^"_x,e^"_y,e^"_z]$$记做旋转矩阵**R**，因此上面的表达式可以简化为$$P^T_C=R\cdot P^T_W$$。接下来是平移部分，假设平移部分是$$P^T_{C^"}$$经过平移向量t后得到$$P^T_{C}$$，那么可以得到$$P^T_C=P^T_{C^"}+t=R\cdot P^T_w+t$$。所以通过旋转矩阵**R**和平移 向量**t**，我们可以描述从世界坐标系到移动机器人坐标系的坐标变换。但是这种表达方式存在一个问题，对于连续的位置变换，例如机器人坐标系是随着时间在不断变换的，上面这种表达方式并不是一个线性的表达方式，假设我们经历了两次变换$$R_1,t_1$$和$$R_2,t_2$$且满足：从a到b的变换$$b=R_1a+t_1$$，从b到c的变换$$c=R_2b+t_2$$.那么从a到c的变换是$$c=R_2(R_1a+t_1)+t_2$$.并不是我们希望的的形式$$c=Ra+t$$(然后我们采用齐次坐标的方式进行表达，详细的部分参考李群李代数).