[TOC] ### **skiplist数据结构简介** skiplist本质上也是一种查找结构，用于解决算法中的查找问题（Searching），即根据给定的key，快速查到它所在的位置（或者对应的value）。 ` ` 一般查找问题的解法分为两个大类：一个是基于各种平衡树，一个是基于哈希表。但skiplist却比较特殊，它没法归属到这两大类里面。 ### **skiplist数据结构演变** skiplist，顾名思义，首先它是一个list。实际上，它是在有序链表的基础上发展起来的。 ` ` **有序链表**，如下图（最左侧的灰色节点表示一个空的头结点）：  ` ` 在这样一个链表中，如果我们要查找某个数据，需要从头开始逐个进行比较，直到找到包含数据的那个节点，或者找到第一个比给定数据大的节点为止（没找到），**时间复杂度为O(n)**；当我们要插入新数据的时候，也要经历同样的查找过程，从而确定插入位置。 ` ` 假如我们每相邻两个节点增加一个指针，让指针指向下下个节点，如下图：  ` ` 这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半（上图中是7, 19, 26）。现在当我们想查找数据的时候，可以先沿着这个新链表进行查找。当碰到比待查数据大的节点时，再回到原来的链表中进行查找。 ` ` 比如，我们想查找23，查找的路径是沿着下图中标红的指针所指向的方向进行的：  ` ` * 23首先和7比较，再和19比较，比它们都大，继续向后比较。 * 但23和26比较的时候，比26要小，因此回到下面的链表（原链表），与22比较。 * 23比22要大，沿下面的指针继续向后和26比较。23比26小，说明待查数据23在原链表中不存在，而且它的插入位置应该在22和26之间。 ` ` 在这个查找过程中，由于新增加的指针，我们不再需要与链表中每个节点逐个进行比较了。**需要比较的节点数大概只有原来的一半**。 ` ` 利用同样的方式，我们可以在上层新产生的链表上，继续为每相邻的两个节点增加一个指针，从而产生第三层链表。如下图：  ` ` 在这个新的三层链表结构上，如果我们还是查找23，那么沿着最上层链表首先要比较的是19，发现23比19大，接下来我们就知道只需要到19的后面去继续查找，从而一下子跳过了19前面的所有节点。可以想象，当链表足够长的时候，这种多层链表的查找方式能让我们跳过很多下层节点，大大加快查找的速度。 >优势：按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似于一个二分查找，使得查找的时间复杂度可以降低到O(log n) 缺点：新插入一个节点之后，就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新蜕化成O(n)。删除数据也有同样的问题。 ` ` skiplist为了避免这一问题，它不要求上下相邻两层链表之间的节点个数有严格的对应关系，而是为**每个节点随机出一个层数(level)**。比如，一个节点随机出的层数是3，那么就把它链入到第1层到第3层这三层链表中。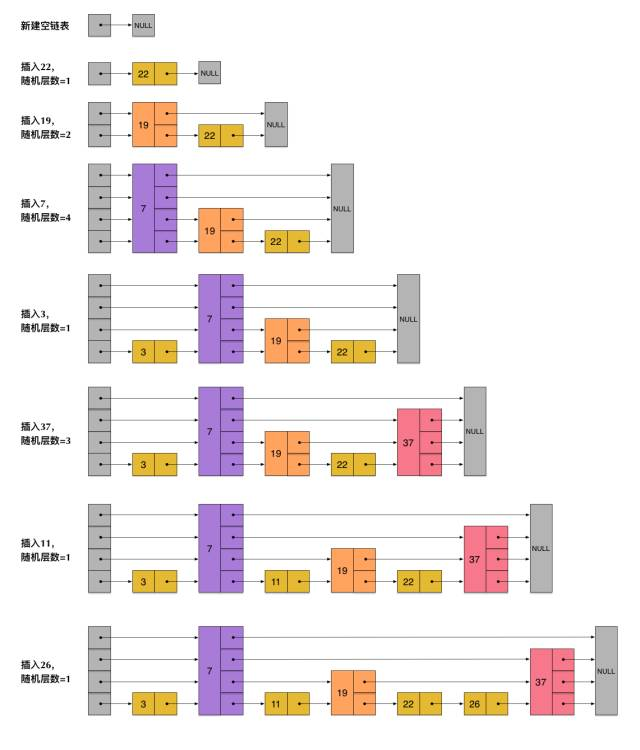为了表达清楚，下图展示了如何通过一步步的插入操作从而形成一个skiplist的过程（点击看大图）：  ` ` **skiplist重要特性**：从上面skiplist的创建和插入过程可以看出，每一个节点的层数（level）是随机出来的，而且新插入一个节点不会影响其它节点的层数。因此，插入操作只需要修改插入节点前后的指针，而不需要对很多节点都进行调整。这就降低了插入操作的复杂度。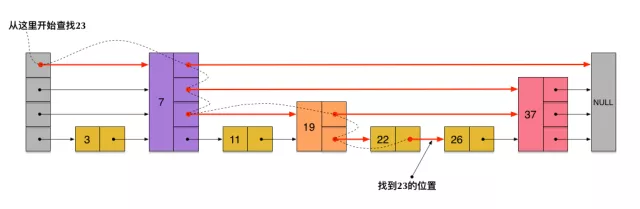**这让它在插入性能上明显优于平衡树的方案** ` ` 刚刚创建的这个skiplist总共包含4层链表，现在假设我们在它里面依然查找23，下图给出了查找路径：  ` ` 前面演示的各个节点的插入过程，实际上在插入之前也要先经历一个类似的查找过程，在确定插入位置后，再完成插入操作, 删除操作与插入操作类似. ` ` #### **随机数计算过程** * 首先，每个节点肯定都有第1层指针（每个节点都在第1层链表里）。 * 如果一个节点有第i层(i>=1)指针（即节点已经在第1层到第i层链表中），那么它有第(i+1)层指针的概率为p。 * 节点最大的层数不允许超过一个最大值，记为MaxLevel。 ` ` 这个计算随机层数的伪码如下所示： ``` randomLevel() level := 1 // random()返回一个[0...1)的随机数 while random() < p and level < MaxLevel do level := level + 1 return level ``` randomLevel()的伪码中包含两个参数，一个是p，一个是MaxLevel。在Redis的skiplist实现中，这两个参数的取值为： ``` p = 1/4MaxLevel = 32 ``` ### skiplist的算法性能分析 ### **skiplist与平衡树、哈希表的比较** * skiplist和各种平衡树（如AVL、红黑树等）的元素是有序排列的，而哈希表不是有序的。因此，在哈希表上只能做单个key的查找，不适宜做范围查找。所谓范围查找，指的是查找那些大小在指定的两个值之间的所有节点。 * 在做范围查找的时候，平衡树比skiplist操作要复杂。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在skiplist上进行范围查找就非常简单，只需要在找到小值之后，对第1层链表进行若干步的遍历就可以实现。 * 平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而skiplist的插入和删除只需要修改相邻节点的指针，操作简单又快速。 * 从内存占用上来说，skiplist比平衡树更灵活一些。一般来说，平衡树每个节点包含2个指针（分别指向左右子树），而skiplist每个节点包含的指针数目平均为1/(1-p)，具体取决于参数p的大小。如果像Redis里的实现一样，取p=1/4，那么平均每个节点包含1.33个指针，比平衡树更有优势。 * 查找单个key，skiplist和平衡树的时间复杂度都为O(log n)，大体相当；而哈希表在保持较低的哈希值冲突概率的前提下，查找时间复杂度接近O(1)，性能更高一些。所以我们平常使用的各种Map或dictionary结构，大都是基于哈希表实现的。 * 从算法实现难度上来比较，skiplist比平衡树要简单得多。