# 前言 现在面试测试岗位，一般会要求熟悉一门语言（python/java），为了考验求职者的基本功，一般会出2个笔试题，这些题目一般不难，主要考察基本功。 要是给你一台电脑，在编辑器里面边写边调试，没多大难度。主要是给你一张纸和笔，让你现场写出来，那就没那么容易了。 （本篇代码都是基于python3.6） <br /> <details> <summary>1. 统计</summary> > 问题1：统计在一个队列中的数字，有多少个正数，多少个负数，如\[1, 3, 5, 7, 0, -1, -9, -4, -5, 8\] #### 方法一 ~~~ # coding:utf-8 a = [1, 3, 5, 7, 0, -1, -9, -4, -5, 8] # 用列表生成式，生成新的列表 b = [i for i in a if i > 0] print("大于0的个数：%s" % len(b)) c = [i for i in a if i < 0] print("小于0的个数：%s" % len(c)) ~~~ #### 方法二 ~~~ # coding:utf-8 a = [1, 3, 5, 7, 0, -1, -9, -4, -5, 8] # 用传统的判断思维，累加 m = 0 n = 0 for i in a: if i > 0: m += 1 elif i < 0: n += 1 else: pass print("大于0的个数：%s" % m) print("小于0的个数：%s" % n) ~~~ </details> <br /> <details> <summary>2. 字符串切片</summary> > 问题1：字符串 "axbyczdj"，如果得到结果“abcd” #### 方法一 ~~~ # 字符串切片 a = "axbyczdj" print(a[::2]) ~~~ #### 方法二 ~~~ # 传统思维 a = "axbyczdj" c = [] for i in range(len(a)): if i % 2 == 0: c.append(a[i]) print("".join(c)) ~~~ </details> <br /> <details> <summary>3. 字符串切割</summary> > 问题：已知一个字符串为“hello\_world\_yoyo”, 如何得到一个队列 \["hello","world","yoyo"\] ~~~ a = "hello_world_yoyo" b = a.split("_") print(b) ~~~ </details> <br /> <details> <summary>4. 格式化输出</summary> > 问题1：已知一个数字为1，如何输出“0001” ~~~ a = 1 print("%04d" % a) ~~~ </details> <br /> <details> <summary>5. 队列</summary> > 问题1：已知一个队列,如： [1, 3, 5, 7], 如何把第一个数字，放到第三个位置，得到：[3, 5, 1, 7] ~~~ a = [1, 3, 5, 7] # insert插入数据 a.insert(3, a[0]) print(a[1:]) ~~~ </details> <br /> <details> <summary>6. 交换</summary> > 问题1：已知 a = 9, b = 8,如何交换a和b的值，得到a的值为8,b的值为9 #### 方法1 ~~~ a = 8 b = 9 a, b = b, a print(a) print(b) ~~~ #### 方法2 ~~~ a = 8 b = 9 # 用中间变量c c = a a = b b = c print(a) print(b) ~~~ </details> <br /> <details> <summary>7. 水仙花</summary> > 问题1：打印出100-999所有的"水仙花数"，所谓"水仙花数"是指一个三位数，其各位数字立方和等于该数本身。例如：153是一个"水仙花数"，因为153=1的三次方＋5的三次方＋3的三次方。 <br /> 方法一 ~~~ sxh = [] for i in range(100, 1000): s = 0 m = list(str(i)) for j in m: s += int(j)**len(m) if i == s: print(i) sxh.append(i) print("100-999的水仙花数：%s" % sxh) ~~~ <br /> 方法二 ``` sxh = [] for i in range(100,1000): s = str(i) if int(s[0])**3+int(s[1])**3+int(s[2])**3 == i: sxh.append(i) print(sxh) ``` </details> <br /> <details> <summary>8. 完全数</summary> > 问题1：如果一个数恰好等于它的因子之和，则称该数为“完全数”，又称完美数或完备数。 例如：第一个完全数是6，它有约数1、2、3、6，除去它本身6外，其余3个数相加， > 1+2+3=6。第二个完全数是28，它有约数1、2、4、7、14、28，除去它本身28外，其余5个数相加，1+2+4+7+14=28。 > 那么问题来了，求1000以内的完全数有哪些？ ~~~ a = [] for i in range(1, 1000): s = 0 for j in range(1, i): if i % j == 0 and j < i: s += j if s == i: print(i) a.append(i) print("1000以内完全数：%s" % a) ~~~ </details> <br /> <details> <summary>9. 冒泡排序</summary> > 冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。 问题1：用python写个冒泡排序 * 方法一： ~~~ a = [1, 3, 10, 9, 21, 35, 4, 6] s = range(1, len(a))[::-1] print(list(s)) # 交换次数 for i in s: for j in range(i): if a[j] > a[j + 1]: a[j], a[j + 1] = a[j + 1], a[j] print("第 %s 轮交换后数据：%s" % (len(s)-i+1, a)) print(a) ~~~ * 方法二 ``` def bubbleSort(arr): n = len(arr) # 遍历所有数组元素 for i in range(n): # 最后一个i元素已经存在 for j in range(0, n - i - 1): if arr[j] > arr[j + 1]: arr[j], arr[j + 1] = arr[j + 1], arr[j] arr = [1, 3, 10, 9, 21, 35, 4, 6] bubbleSort(arr) print("排序后的数组:") for i in range(len(arr)): print("%d" % arr[i]) ``` </details> <br /> <details> <summary>10. sort排序</summary> > 问题1：已知一个队列\[1, 3, 6, 9, 7, 3, 4, 6\] * 按从小到大排序 * 按从大大小排序 * 去除重复数字 ~~~ a = [1, 3, 6, 9, 7, 3, 4, 6] # 1.sort排序，正序 a.sort() print(a) # 2.sort倒叙 a.sort(reverse=True) print(a) # 3.去重 b = list(set(a)) print(b) ~~~ </details> <br /> <details> <summary>11. 计算n的阶乘</summary> > 问题1：计算n!,例如n=3(计算3*2*1=6)， 求10! #### 方法1：可以用python里面的reduce函数，reduce() 函数会对参数序列中元素进行累积。 函数将一个数据集合（链表，元组等）中的所有数据进行下列操作：用传给 reduce 中的函数 function（有两个参数）先对集合中的第 1、2 个元素进行操作，得到的结果再与第三个数据用 function 函数运算，最后得到一个结果。 ~~~ from functools import reduce # 方法1：推荐！ a = 10 b = reduce(lambda x, y: x*y, range(1, a+1)) print(b) ~~~ 如果不想用lamdba函数，可以定义一个函数 ~~~ from functools import reduce def chengfa(x, y): return x*y a = 10 b = reduce(chengfa, range(1, a+1)) print(b) ~~~ #### 方法2：自己写个递归函数 ~~~ def digui(n): if n == 1: return 1 else: return n*digui(n-1) a = 10 print(digui(a)) ~~~ #### 方法3：用for循环（不推荐！） ~~~ a = 10 s = 1 for i in range(1, a+1): s = s*i print(s) ~~~ </details> <br /> <details> <summary>12. 斐波那契数列</summary> <br /> > 问题1：已知一个数列：1、1、2、3、5、8、13.....的规律为从3开始的每一项都等于其前两项的和，这是斐波那契数列。求满足规律的100以内的所有数据 ~~~ a = 0 b = 1 while b < 100: print(b, end=",") a, b = b, a+b ~~~ </details> <br /> <details> <summary>13. 幂的递归</summary> <br /> 计算x的n次方，如：3的4次方 为3\*3\*3\*3=81 ~~~ def mi(x, n): '''计算x 的n 次方''' if n == 0: return 1 else: return x*mi(x, n-1) x = 3 num = 4 print(mi(x, num)) ~~~ </details> <br /> <details> <summary>14. 汉诺塔问题(一般不会考)</summary> <br /> 汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。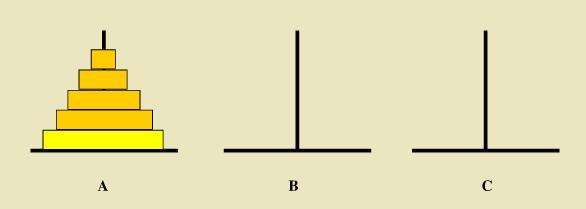并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘  当只有一个盘子的时候，只需要从将A塔上的一个盘子移到C塔上。 当A塔上有两个盘子是，先将A塔上的1号盘子（编号从上到下）移动到B塔上，再将A塔上的2号盘子移动的C塔上，最后将B塔上的小盘子移动到C塔上。 当A塔上有3个盘子时，先将A塔上编号1至2的盘子（共2个）移动到B塔上（需借助C塔），然后将A塔上的3号最大的盘子移动到C塔，最后将B塔上的两个盘子借助A塔移动到C塔上。 当A塔上有n个盘子是，先将A塔上编号1至n-1的盘子（共n-1个）移动到B塔上（借助C塔），然后将A塔上最大的n号盘子移动到C塔上，最后将B塔上的n-1个盘子借助A塔移动到C塔上。 综上所述，除了只有一个盘子时不需要借助其他塔外，其余情况均一样（只是事件的复杂程度不一样）。 ~~~ def hanoi(n, a, b, c): '''汉诺塔问题''' if n == 1: print(a, '-->', c) else: hanoi(n - 1, a, c, b) print(a, '-->', c) hanoi(n - 1, b, a, c) hanoi(5, 'A', 'B', 'C') ~~~ 一般汉诺塔问题不会经常考，前面几个考的比较频繁 </details> <br /> <details> <summary>15. 对列表list去重</summary> <br /> 方法一：直接的方法 ``` old_list = [2, 3, 4, 5, 1, 2, 3] new_list = [] for i in old_list: if i not in new_list: new_list.append(i) print(new_list) # [2, 3, 4, 5, 1] ``` </details> <br /> <details> <summary>16. 如何判断三角形的类型</summary> ``` a = int(input("请输入第一条边:")) b = int(input("请输入第二条边:")) c = int(input("请输入第三条边:")) if (a+b>c) and (a+c>b) and (b+c>a): if a==b==c: print("等边三角形") elif (a==b or b==c or a==c): print("等腰三角形") elif (a*a + b*b == c*c) or (a*a + c*c == b*b) or (b*b + c*c == a*a): print("直角三角形") else: print("不规则三角形") else: print("不是三角形") ``` </details> <br />