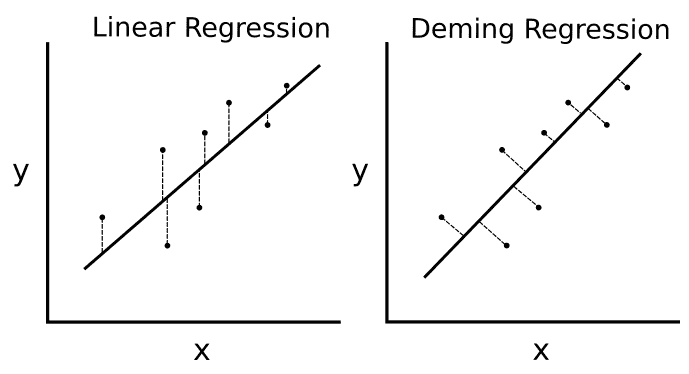
# 实现 deming 回归 在这个秘籍中，我们将实现 deming 回归，这意味着我们需要一种不同的方法来测量模型线和数据点之间的距离。 > 戴明回归有几个名字。它也称为总回归，正交距离回归（ODR）和最短距离回归。 ## 做好准备 如果最小二乘线性回归最小化到线的垂直距离，则 deming 回归最小化到线的总距离。这种类型的回归可以最小化`y`和`x`值的误差。 请参阅下图进行比较：  图 8：常规线性回归和 deming 回归之间的差异;左边的线性回归最小化了到线的垂直距离，右边的变形回归最小化了到线的总距离 要实现 deming 回归，我们必须修改损失函数。常规线性回归中的损失函数使垂直距离最小化。在这里，我们希望最小化总距离。给定线的斜率和截距，到点的垂直距离是已知的几何公式​​。我们只需要替换此公式并告诉 TensorFlow 将其最小化。 ## 操作步骤 我们按如下方式处理秘籍： 1. 代码与之前的秘籍非常相似，除非我们进入损失函数。我们首先加载库;开始一个会议;加载数据;声明批量大小;并创建占位符，变量和模型输出，如下所示： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn import datasets sess = tf.Session() iris = datasets.load_iris() x_vals = np.array([x[3] for x in iris.data]) y_vals = np.array([y[0] for y in iris.data]) batch_size = 50 x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) A = tf.Variable(tf.random_normal(shape=[1,1])) b = tf.Variable(tf.random_normal(shape=[1,1])) model_output = tf.add(tf.matmul(x_data, A), b) ``` 1. 损失函数是由分子和分母组成的几何公式​​。为清楚起见，我们将分别编写这些内容。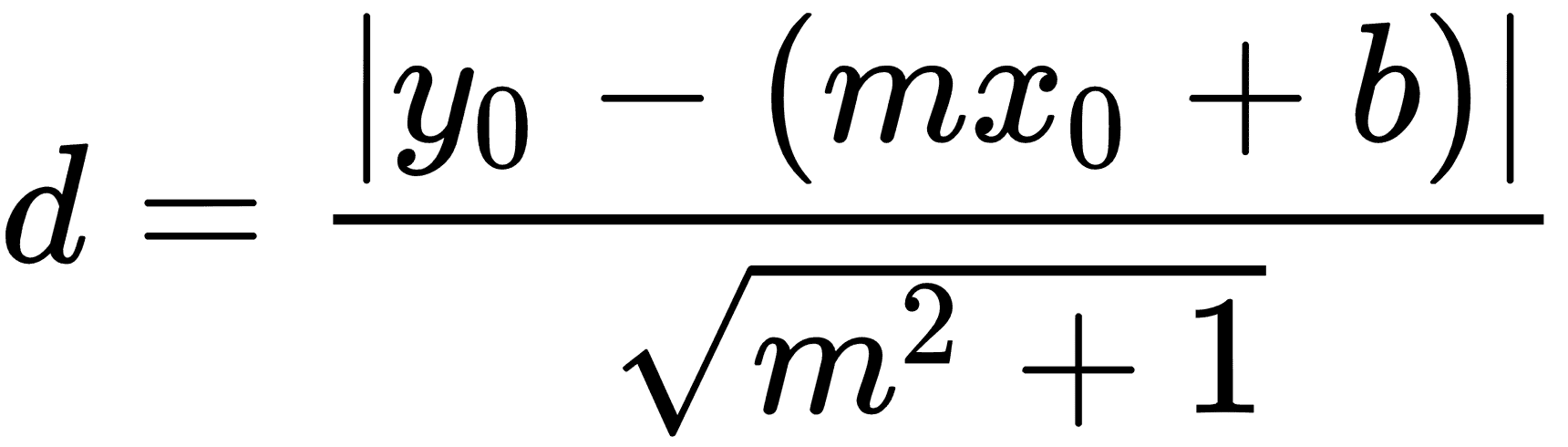给定一条线`y = mx + b`和一个点`(x0, y0)`，两者之间的垂直距离可以写成如下：  ```py deming_numerator = tf.abs(tf.sub(y_target, tf.add(tf.matmul(x_data, A), b))) deming_denominator = tf.sqrt(tf.add(tf.square(A),1)) loss = tf.reduce_mean(tf.truediv(deming_numerator, deming_denominator)) ``` 1. 我们现在初始化变量，声明我们的优化器，并循环遍历训练集以获得我们的参数，如下所示： ```py init = tf.global_variables_initializer() sess.run(init) my_opt = tf.train.GradientDescentOptimizer(0.1) train_step = my_opt.minimize(loss) loss_vec = [] for i in range(250): rand_index = np.random.choice(len(x_vals), size=batch_size) rand_x = np.transpose([x_vals[rand_index]]) rand_y = np.transpose([y_vals[rand_index]]) sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec.append(temp_loss) if (i+1)%50==0: print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b))) print('Loss = ' + str(temp_loss)) ``` 1. 我们可以使用以下代码绘制输出： ```py [slope] = sess.run(A) [y_intercept] = sess.run(b) best_fit = [] for i in x_vals: best_fit.append(slope*i+y_intercept) plt.plot(x_vals, y_vals, 'o', label='Data Points') plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3) plt.legend(loc='upper left') plt.title('Sepal Length vs petal Width') plt.xlabel('petal Width') plt.ylabel('Sepal Length') plt.show() ``` 我们得到上面代码的以下图：  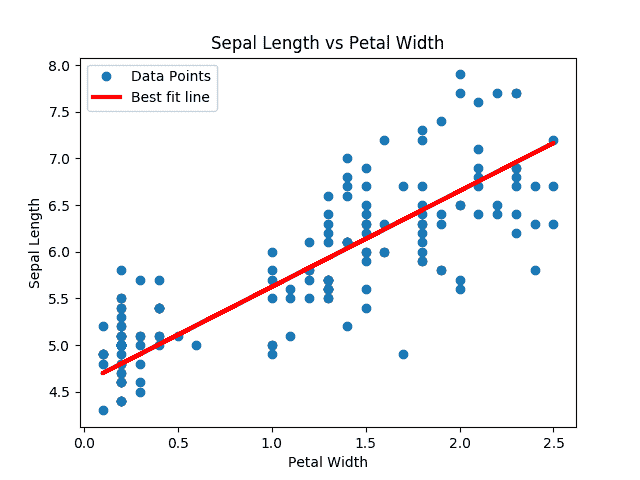图 9：对虹膜数据集进行 deming 回归的解决方案 ## 工作原理 deming 回归的方法几乎与常规线性回归相同。关键的区别在于我们如何衡量预测和数据点之间的损失。而不是垂直损失，我们对`y`和`x`值有垂直损失（或总损失）。 > 当我们假设`x`和`y`值中的误差相似时，使用这种类型的回归。根据我们的假设，我们还可以根据误差的差异在距离计算中缩放`x`和`y`轴。