## 希腊与古希腊 希腊共和国，也就是希腊，是欧洲东南角、巴尔干半岛南端的一个共和国国家。希腊其历史可以追溯到古希腊，但古希腊不是一个独立的国家，而是一个地区的称谓。其位于欧洲东南部、地中海的东北部，由希腊半岛、爱琴海和爱奥尼亚海上群岛、意大利东部的西西里岛东部沿岸地区组成。从地理上看， 古希腊包含的地域范围比现在的希腊共和国要大。 ## 古希腊文明 古希腊是西方文明的源头之一，也是最重要和最直接的源头。但其不是一个国家，理所应当也不是四大文明古国之一。常听见的古希腊文明的典型代表有： * 历史： 1. 希波战争： 希腊人与波斯人的战争 * 文化 1. 希腊神话，十二大主神， 宙斯、雅典娜、阿波罗等 2. 《荷马史诗》 3. 《伊索寓言》 4. 哲学：苏格拉底、柏拉图、亚里斯多德 ## 古希腊字母 在希腊字母之前，古希腊人使用称为"线性文字A" "线性文字B" 的符号来记录。大约公元前900年，腓尼基字母传入希腊，希腊人在其基础上又创造了四个字母，形成了24个字母的字母表。 24 在古希腊文明中有着特别的含义。 线性文字一瞥：  腓尼基字母的样貌如下：  希腊字母的起源来自于基本的生活需求，后来被广泛应用在数学、科学、物理等领域。 ## 希腊字母、拉丁字母等字母体系的关系 古希腊文明曾经辉煌一时，但在历史的长河中逐步的衰落、黯淡。不过其影响还是深远的。 当今世界的三大字母体系是： 1. 拉丁字母：欧美国家， 美国、英国等 2. 阿拉伯字母：西亚及阿拉伯国家， 比如埃及、苏丹等 3. 斯拉夫字母 ：俄国、南斯拉夫 这三种字母源头都来自于腓尼基字母，所以腓尼基字母也称为字母之源。 #### 拉丁字母 拉丁字母由希腊字母间接发展而来，是古罗马人的文字（约公元前7世纪～前6世纪）。古罗马灭亡前包含23个字母。其中 * 18个辅音字母： B、C、D、F、G、Z、H、K、L、M、N、P、Q、R、S、T、X、Y * 4个原音字母：A、E、I、O 11世纪时增加了J、U、W， 总共26个字母。 拉丁字母：源自希腊字母，由意大利半岛最早的岛民拉丁人创造。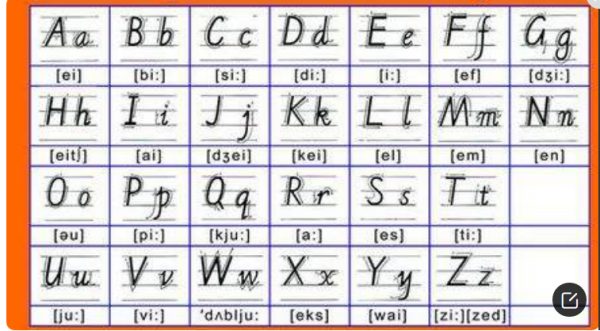拉丁文后来成了罗马文字，又称为“罗马字母”  #### 阿拉伯字母 是西亚阿拉伯地区及部分穆斯林国家和穆斯林教徒使用的字母。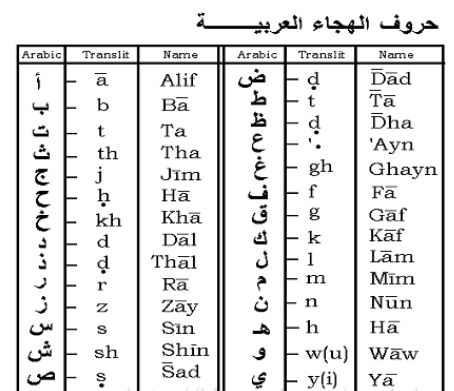  #### 斯拉夫字母 斯拉夫字母（也称西里尔字母）：罗马帝国分裂后，东罗马传教士西里尔为了在斯拉夫地区传播东正教，在希腊字母的基础上创造出西里尔字母，用来拼写斯拉夫人的语言。俄语就是该字母的代表。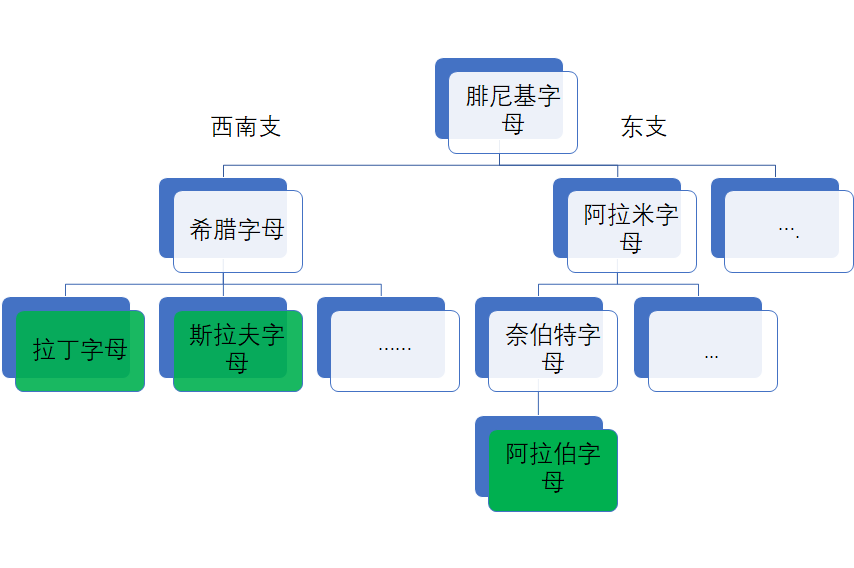  #### 各字母体系的继承关系 西里尔字母各地区有差异，拉丁字母有统一的国际标准。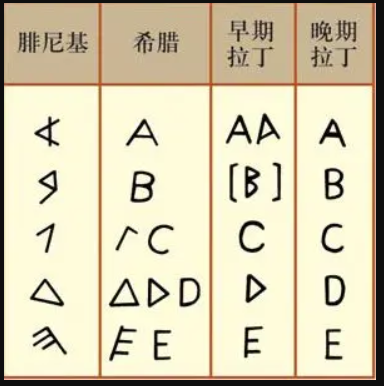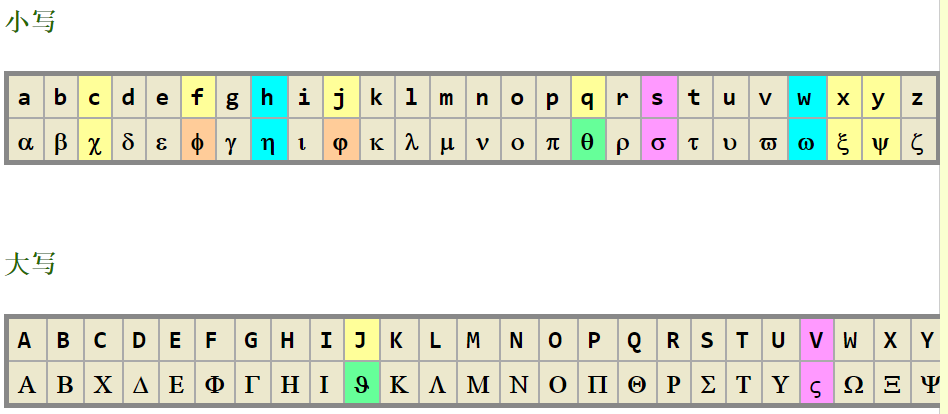  #### 各字母体系的对应关系 * 腓尼基字母 VS 希腊 VS 拉丁 的对应示例  * 希腊字母与拉丁字母的完整对应  #### 汉语拼音 很多相对复杂的语言，都采用字母来拼写自己的语言。 汉语拼音：现代汉语拼音使用的是拉丁字母。 汉语拼音曾经计划用西里尔字母，但因为中苏关系紧张，最终选择了拉丁字母。 ## 希腊字母的写法和读法 希腊字母有24个， 区分大小写。 | 序号 | 大写 | 小写 |英文注音 |中文注音 | 意义| | --- | --- |--- |--- |--- |--- | | 1 | Α | α| alpha | 阿尔法 | 角度、系数 | | 2 | Β | β | beta |贝塔 | 磁通系数；角度、系数 | | 3 | Γ | γ |gamma |伽玛 |电导系数 | | 4 | Δ | δ | delta |德尔塔 | 变动；密度、屈光度 | | 5 | Ε | ε | epsilon | 伊普西龙 |对数之基数；介电常数 | | 6 | Ζ | ζ | zeta| 截塔 | 系数；方位角、阻抗、相对粘度 | | 7 | Η | η | eta| 艾塔 | 迟滞系数。效率 | | 8 | Θ | θ | thet| 西塔 | 温度，角度 | | 9 | Ι | ι | iot |约塔 | 微小，一点| | 10 | Κ |κ | kappa| 卡帕 | 介质常数，绝热指数 | | 11 | ∧ | λ |lambda | 兰布达|波长，体积，导热系数 | | 12 | Μ | μ | mu | 缪 |磁导系数，动摩系数，流体粘度 | | 13 | Ν | φ | nu | 纽 | 磁阻系数，动力粘度| | 14 | Ξ | ξ | xi | 克西 | 随机数，区间内的一个未知的特定值| | 15 | Ο |ο |omicron | 奥密克戎 | 高阶无穷小函数 | | 16 | ∏ |π | pi|派 | 圆周率 | | 17 | Ρ | ρ |rho | 肉| 电阻系数，柱坐标和极坐标中的极径，密度 | | 18 | ∑ |σ | sigma | 西格玛 | 总和，表面密度，跨导，正应力| | 19 | Τ | τ | tau| 套| 时间常数，切应力 | | 20 | Υ | υ| upsilon |宇普西龙 | 位移 | | 21 | Φ | φ | phi|佛爱 | 磁通，角，透镜角度，热流量 | | 22 | Χ | χ | chi |西 | 统计学有卡方分布 `$ χ^2 $` | | 23 | Ψ| ψ | psi | 普西 | 角速，介质电通量 | | 24 | Ω | ω |omega | 欧米茄 | 欧姆，角速度，交流电的电角度 | ***** ***** * Α α alpha a:lf 阿尔法 角度；系数 * Β β beta bet 贝塔 磁通系数；角度；系数 * Γ γ gamma ga:m 伽马 电导系数（小写） * Δ δ delta delt 德尔塔 变动；密度；屈光度 * Ε ε epsilon ep`silon 伊普西龙 对数之基数 * Ζ ζ zeta zat 截塔 系数；方位角；阻抗；相对粘度；原子序数 * Η η eta eit 艾塔 磁滞系数；效率（小写） * Θ θ thet θit 西塔 温度；相位角 * Ι ι iot aiot 约塔 微小,一点儿 * Κ κ kappa kap 卡帕 介质常数 * ∧ λ lambda lambd 兰布达波长（小写）；体积 * Μ μ mu mju 缪 磁导系数；微（千分之一）；放大因数（小写） * Ν ν nu nju 纽 磁阻系数 * Ξ ξ xi ksi 克西 * Ο ο omicron omik`ron 奥密克戎 * ∏ π pi pai 派 圆周率=圆周÷直径=3.1416 * Ρ ρ rho rou 肉 电阻系数（小写） * ∑ σ sigma `sigma 西格马 总和（大写）,表面密度；跨导（小写） * Τ τ tau tau 套 时间常数 * Υ υ upsilon jup`silon 宇普西龙 位移 * Φ φ phi fai 佛爱 磁通；角 * Χ χ chi phai 西 * Ψ ψ psi psai 普西 角速；介质电通量（静电力线）；角 * ∈ * Ω ω omega o`miga 欧米伽 欧姆（大写）；角速（小写）；角 * ξ xi ksi 克西 具体如下 * ∞ * ∫ * λ