查找最大数为 1 的二进制矩阵的行号 · GeeksForGeeks 中文系列教程

# 查找最大数为 1 的二进制矩阵的行号 > 原文： [https://www.geeksforgeeks.org/find-row-number-binary-matrix-maximum-number-1s/](https://www.geeksforgeeks.org/find-row-number-binary-matrix-maximum-number-1s/) 给定 n * n 阶的二进制矩阵（仅包含 0 和 1）。所有行均已排序，我们需要找到最大为 1s 的行号。还要在该行中找到数字 1。注意：如果是平局，则打印较小的行号。 **示例**： ``` Input : mat[3][3] = {0, 0, 1, 0, 1, 1, 0, 0, 0} Output : Row number = 2, MaxCount = 2 Input : mat[3][3] = {1, 1, 1, 1, 1, 1, 0, 0, 0} Output : Row number = 1, MaxCount = 3 ``` **基本方法**：遍历整个矩阵，并为每行找到 1 的数目，并在所有行中不断更新最大数目为 1 的行号。此方法将导致 O（n ^ 2）时间复杂度。 **更好的方法**：如果我们尝试应用二分搜索来查找每行中第一个 1 的位置，并且随着对每一行进行排序就可以从每行中找到 1 的数目，那么我们可以做得更好订购。这将导致 O（nlogn）时间复杂度。 **有效方法**：从索引（1，n）的左上角开始，尝试向左移动直到到达该行（第 j 列）的最后 1 个，现在如果我们向左移动到该行，我们将找到 0，因此切换到同一列的正下方。现在，如果第 j 个元素（如果 1）尝试向左移动，则您的位置将再次位于第二行（2，j），直到找到最后 1 个；否则，如果第 j 个元素为 0，则在第二行中转到下一行。因此，最后要说的是，如果您位于第 ith 行和第 j 列中的任何一个，即该行右边的最后 1 个索引，则递增 i。因此，现在如果 Aij = 0 再次增加 i，否则继续减少 j，直到在该特定行中找到最后 1 个为止。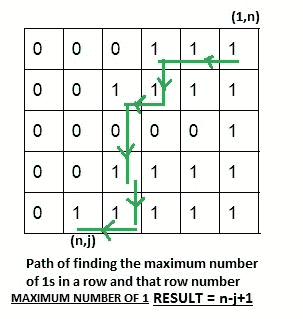示例图： ![](https://img.kancloud.cn/5d/ac/5dace99475cdd853bc4852b9ede525bd_303x319.png) **算法**： ``` for (int i=0, j=n-1; i<n;i++) { // find left most position of 1 in a row // find 1st zero in a row while (arr[i][j]==1) { row = i; j--; } } cout << "Row number =" << row+1; cout << "MaxCount =" << n-j; ``` ## C++ ```cpp // CPP program to find row with maximum 1 // in row sorted binary matrix #include<bits/stdc++.h> #define N 4 using namespace std; // function for finding row with maximum 1 void findMax (int arr[][N]) { int row = 0, i, j; for (i=0, j=N-1; i<N;i++) { // find left most position of 1 in a row // find 1st zero in a row while (arr[i][j] == 1 && j >= 0) { row = i; j--; } } cout << "Row number = " << row+1; cout << ", MaxCount = " << N-1-j; } // driver program int main() { int arr[N][N] = {0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1}; findMax(arr); return 0; } ``` ## Java ```java // Java program to find row with maximum 1 // in row sorted binary matrix class GFG { static final int N = 4; // function for finding row with maximum 1 static void findMax(int arr[][]) { int row = 0, i, j; for (i = 0, j = N - 1; i < N; i++) { // find left most position of 1 in // a row find 1st zero in a row while (j >= 0 && arr[i][j] == 1) { row = i; j--; } } System.out.print("Row number = " + (row + 1)); System.out.print(", MaxCount = " + (N - 1 - j)); } // Driver code public static void main(String[] args) { int arr[][] = {{0, 0, 0, 1}, {0, 0, 0, 1}, {0, 0, 0, 0}, {0, 1, 1, 1}}; findMax(arr); } } // This code is contributed by Anant Agarwal. ``` ## Python3 ```py # python program to find row with # maximum 1 in row sorted binary # matrix N = 4 # function for finding row with # maximum 1 def findMax (arr): row = 0 j = N - 1 for i in range(0, N): # find left most position # of 1 in a row find 1st # zero in a row while (arr[i][j] == 1 and j >= 0): row = i j -= 1 print("Row number = " , row + 1, ", MaxCount = ", N - 1 - j) # driver program arr = [ [0, 0, 0, 1], [0, 0, 0, 1], [0, 0, 0, 0], [0, 1, 1, 1] ] findMax(arr) # This code is contributed by Sam007 ``` ## C# ```cs // C# program to find row with maximum // 1 in row sorted binary matrix using System; class GFG { static int N = 4; // function for finding row with maximum 1 static void findMax(int [,]arr) { int row = 0, i, j; for (i = 0, j = N - 1; i < N; i++) { // find left most position of 1 in // a row find 1st zero in a row while (arr[i,j] == 1 && j >= 0) { row = i; j--; } } Console.Write("Row number = " + (row + 1)); Console.Write(", MaxCount = " + (N - 1 - j)); } // Driver code public static void Main() { int [,]arr = {{0, 0, 0, 1}, {0, 0, 0, 1}, {0, 0, 0, 0}, {0, 1, 1, 1}}; findMax(arr); } } // This code is contributed by nitin mittal ``` ## PHP ```php <?php // PHP program to find // row with maximum 1 // in row sorted // binary matrix $N = 4; // function for finding // row with maximum 1 function findMax ($arr) { global $N; $row = 0; $i; $j=$N - 1; for ($i = 0; $i < $N; $i++) { // find left most position // of 1 in a row find 1st // zero in a row while ($arr[$i][$j] == 1 && $j >= 0) { $row = $i; $j--; } } echo "Row number = " , $row + 1; echo ", MaxCount = " , $N - 1 - $j; } // Driver Code $arr = array(array(0, 0, 0, 1), array(0, 0, 0, 1), array(0, 0, 0, 0), array(0, 1, 1, 1)); findMax($arr); // This code is contributed by vt_m. ?> ``` Output: ``` Row number = 4, MaxCount = 3 ``` 本文由 [**Shivam Pradhan（anuj_charm）**](http://www.facebook.com/ma5ter6it) 提供。如果您喜欢 GeeksforGeeks 并希望做出贡献，则还可以使用 [tribution.geeksforgeeks.org](http://www.contribute.geeksforgeeks.org) 撰写文章，或将您的文章邮寄至 tribution@geeksforgeeks.org。查看您的文章出现在 GeeksforGeeks 主页上，并帮助其他 Geeks。