## 4.2 使用表格汇总数据 总结数据的一个简单方法是生成一个表，表示各种类型观测的计数。这种类型的表已经使用了数千年（见图[4.1](#fig:salesContract)）。  图 4.1 卢浮宫的苏美尔平板电脑，显示房屋和田地的销售合同。公共领域，通过维基共享资源。 让我们来看一些使用表的例子，同样使用 nhanes 数据集。在 rstudio 控制台中键入命令`help(NHANES)`，然后滚动查看帮助页面，如果使用 rstudio，该页面将在帮助面板中打开。此页提供有关数据集的一些信息以及数据集中包含的所有变量的列表。让我们来看一个简单的变量，在数据集中称为“physactive”。此变量包含三个不同值中的一个：“是”或“否”（指示此人是否报告正在进行“中等强度或剧烈强度的运动、健身或娱乐活动”），如果该个人缺少数据，则为“不”。有不同的原因导致数据丢失；例如，这一问题不是针对 12 岁以下的儿童提出的，而在其他情况下，成人可能在采访期间拒绝回答这个问题。 ### 4.2.1 频率分布 让我们看看每个类别中有多少人。现在不要担心 R 到底是怎么做的，我们稍后再谈。 ```r # summarize physical activity data PhysActive_table <- NHANES %>% dplyr::select(PhysActive) %>% group_by(PhysActive) %>% summarize(AbsoluteFrequency = n()) pander(PhysActive_table) ``` <colgroup><col style="width: 18%"> <col style="width: 26%"></colgroup> | 物理激活 | 绝对频率 | | --- | --- | | 不 | 2473 个 | | 是的 | 2972 年 | | 不适用 | 1334 年 | 此单元格中的 r 代码生成一个表格，显示每个不同值的频率；有 2473 名回答“否”的人，2972 名回答“是”，1334 名没有回答。我们称之为 _ 频率分布 _，因为它告诉我们每个值是如何分布在样本中的。 因为我们只想与回答问题的人一起工作，所以让我们过滤数据集，使其只包括回答此问题的个人。 ```r # summarize physical activity data after dropping NA values using drop_na() NHANES %>% drop_na(PhysActive) %>% dplyr::select(PhysActive) %>% group_by(PhysActive) %>% summarize(AbsoluteFrequency = n()) %>% pander() ``` <colgroup><col style="width: 18%"> <col style="width: 26%"></colgroup> | PhysActive | AbsoluteFrequency | | --- | --- | | No | 2473 | | Yes | 2972 | 这向我们展示了两个响应的绝对频率，对于每个实际给出响应的人。从这一点上我们可以看出，说“是”的人比说“不”的人多，但从绝对数上很难分辨出差别有多大。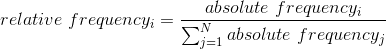因此，我们通常希望使用 _ 相对频率 _ 来呈现数据，该相对频率是通过将每个频率除以所有频率的和得到的：  在 R 中我们可以这样做，如下所示： ```r # compute relative frequency of physical activity categories NHANES %>% drop_na(PhysActive) %>% dplyr::select(PhysActive) %>% group_by(PhysActive) %>% summarize(AbsoluteFrequency = n()) %>% mutate(RelativeFrequency = AbsoluteFrequency / sum(AbsoluteFrequency)) %>% pander() ``` <colgroup><col style="width: 18%"> <col style="width: 27%"> <col style="width: 27%"></colgroup> | PhysActive | AbsoluteFrequency | 相对频率 | | --- | --- | --- | | No | 2473 | 0.454 个 | | Yes | 2972 | 0.546 个 | 相对频率提供了一种更简单的方法来判断不平衡的程度。我们还可以通过将相对频率乘以 100 来将其解释为百分比： ```r # compute percentages for physical activity categories PhysActive_table_filtered <- NHANES %>% drop_na(PhysActive) %>% dplyr::select(PhysActive) %>% group_by(PhysActive) %>% summarize(AbsoluteFrequency = n()) %>% mutate( RelativeFrequency = AbsoluteFrequency / sum(AbsoluteFrequency), Percentage = RelativeFrequency * 100 ) pander(PhysActive_table_filtered) ``` <colgroup><col style="width: 18%"> <col style="width: 27%"> <col style="width: 27%"> <col style="width: 16%"></colgroup> | PhysActive | AbsoluteFrequency | RelativeFrequency | 百分比 | | --- | --- | --- | --- | | No | 2473 | 0.454 | 45.418 美元 | | Yes | 2972 | 0.546 | 54.582 条 | 这让我们看到，NHANES 样本中 45.42%的人说“不”，54.58%的人说“是”。 ### 4.2.2 累积分布 我们在上面研究的 physactive 变量只有两个可能的值，但我们通常希望总结出可以有更多可能值的数据。当这些值至少是序数时，总结它们的一个有用方法是通过我们所称的 _ 累积 _ 频率表示：我们不询问对特定值进行多少观察，而是询问有多少个值至少是 _ 某个特定值。_ 让我们看一下 nhanes 数据集中的另一个变量，名为 sleephrsnight，它记录了参与者在正常工作日报告睡眠的时间。让我们像上面一样创建一个频率表，在删除了没有对问题作出响应的任何人之后。 ```r # create summary table for relative frequency of different # values of SleepHrsNight NHANES %>% drop_na(SleepHrsNight) %>% dplyr::select(SleepHrsNight) %>% group_by(SleepHrsNight) %>% summarize(AbsoluteFrequency = n()) %>% mutate( RelativeFrequency = AbsoluteFrequency / sum(AbsoluteFrequency), Percentage = RelativeFrequency * 100 ) %>% pander() ``` <colgroup><col style="width: 22%"> <col style="width: 27%"> <col style="width: 27%"> <col style="width: 16%"></colgroup> | 睡眠之光 | AbsoluteFrequency | RelativeFrequency | Percentage | | --- | --- | --- | --- | | 二 | 9 | 0.002 个 | 0.179 个 | | 三 | 49 岁 | 0.01 分 | 0.973 个 | | 4 | 200 个 | 0.04 分 | 3.972 年 | | 5 个 | 406 个 | 0.081 个 | 8.064 年 | | 6 | 1172 年 | 0.233 个 | 23.277 页 | | 7 | 1394 年 | 0.277 个 | 27.686 年 | | 8 个 | 1405 年 | 0.279 个 | 27.905 年 | | 9 | 271 个 | 0.054 个 | 5.382 条 | | 10 个 | 97 | 0.019 个 | 1.927 个 | | 11 个 | 15 个 | 0.003 个 | 0.298 个 | | 12 个 | 17 | 0.003 | 0.338 个 | 我们可以通过查看表开始汇总数据集；例如，我们可以看到大多数人报告睡眠时间在 6 到 8 小时之间。让我们绘制数据以更清楚地看到这一点。要做到这一点，我们可以绘制一个 _ 柱状图 _，它显示具有每个不同值的事例数；请参见图[4.2](#fig:sleepHist)的左面板。ggplot2（）库有一个内置的柱状图函数（`geom_histogram()`），我们经常使用它。我们还可以绘制相对频率，我们通常将其称为 _ 密度 _——参见图[4.2](#fig:sleepHist)的右面板。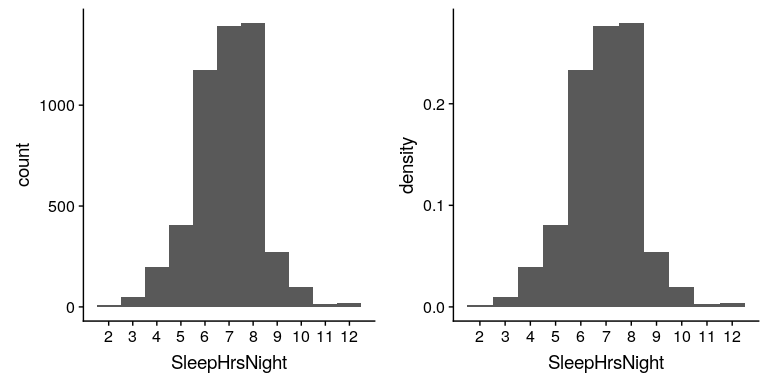  图 4.2 左：显示报告 sleephrsnight 变量每个可能值的人数（左）和比例（右）的柱状图。 如果我们想知道有多少人报告睡眠 5 小时或更少怎么办？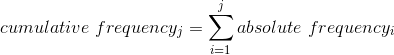为了找到这个，我们可以计算一个 _ 累积分布 _：  也就是说，为了计算某个值 j 的累积频率，我们将所有值（包括 j）的频率相加。让我们对睡眠变量进行计算，首先对绝对频率进行计算： ```r # create cumulative frequency distribution of SleepHrsNight data SleepHrsNight_cumulative <- NHANES %>% drop_na(SleepHrsNight) %>% dplyr::select(SleepHrsNight) %>% group_by(SleepHrsNight) %>% summarize(AbsoluteFrequency = n()) %>% mutate(CumulativeFrequency = cumsum(AbsoluteFrequency)) pander(SleepHrsNight_cumulative) ``` <colgroup><col style="width: 22%"> <col style="width: 27%"> <col style="width: 29%"></colgroup> | SleepHrsNight | AbsoluteFrequency | 累积频率 | | --- | --- | --- | | 2 | 9 | 9 | | 3 | 49 | 58 | | 4 | 200 | 258 个 | | 5 | 406 | 664 个 | | 6 | 1172 | 1836 年 | | 7 | 1394 | 3230 个 | | 8 | 1405 | 4635 个 | | 9 | 271 | 4906 个 | | 10 | 97 | 5003 个 | | 11 | 15 | 5018 年 | | 12 | 17 | 5035 个 | 在图[4.3](#fig:sleepAbsCumulRelFreq)的左侧面板中，我们绘制了数据，以查看这些表示形式的外观；绝对频率值以红色绘制，累积频率以蓝色绘制。我们看到累积频率是单调递增的，也就是说，它只能上升或保持不变，但不能下降。同样，我们通常发现相对频率比绝对频率更有用；这些频率绘制在图[4.3](#fig:sleepAbsCumulRelFreq)的右面板中。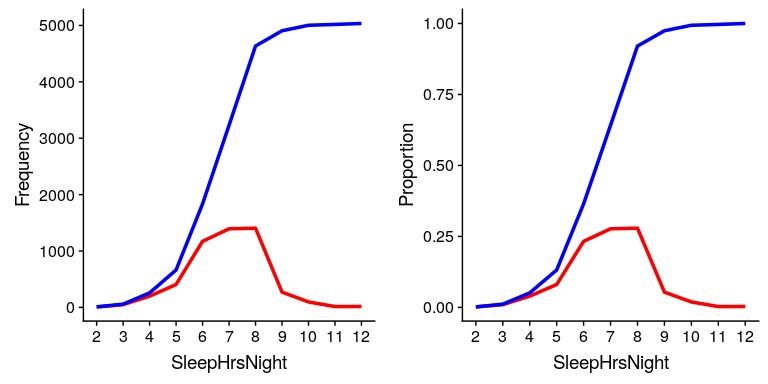  图 4.3 SleephrsNight 可能值的频率（左）和比例（右）的相对（红）和累积相对（蓝）值的图。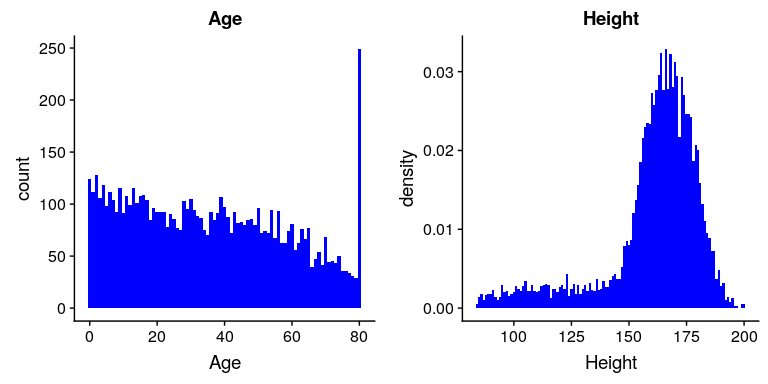 ### 4.2.3 绘制柱状图  图 4.4 nhanes 中年龄（左）和身高（右）变量的柱状图。 我们在上面研究的变量相当简单，只有几个可能的值。现在让我们来看一个更复杂的变量：年龄。首先，让我们绘制 nhanes 数据集中所有个体的年龄变量（参见图[4.4](#fig:ageHist)的左面板）。你看到了什么？首先，你应该注意到每个年龄组的个体数量随着时间的推移而减少。这是有道理的，因为人口是随机抽样的，因此随着时间的推移死亡导致老年人的数量减少。其次，你可能在 80 岁的时候注意到图表中有一个大的尖峰。你觉得这是怎么回事？ 如果您查看 nhanes 数据集的帮助功能，您将看到以下定义：“研究参与者筛选的年龄（年）。注：80 岁或 80 岁以上的受试者被记录为 80 岁。“原因在于，年龄很高的受试者数量相对较少，如果你知道他们的确切年龄，就可能更容易在数据集中识别出特定的人；研究人员通常承诺他们的参与蚂蚁要对自己的身份保密，这是他们能做的有助于保护研究对象的事情之一。这也突显了一个事实，即知道一个人的数据来自何处以及如何处理它们总是很重要的；否则，我们可能会不正确地解释它们。 让我们看看 nhanes 数据集中另一个更复杂的变量：高度。高度值的柱状图绘制在图[4.4](#fig:ageHist)的右面板中。关于这个分布你首先应该注意的是，它的大部分密度集中在 170 厘米左右，但是分布的左侧有一个“尾巴”；有少数个体的高度要小得多。你觉得这是怎么回事？ 您可能已经直觉到小高度来自数据集中的子级。检查这一点的一种方法是为儿童和成人绘制单独颜色的柱状图（图[4.5](#fig:heightHistSep)的左面板）。这表明，所有非常短的高度确实来自样本中的儿童。让我们创建一个新版本的 nhanes，它只包含成年人，然后为他们绘制柱状图（图[4.5](#fig:heightHistSep)的右面板）。在这个图中，分布看起来更加对称。正如我们稍后将看到的，这是一个 _ 正态 _（或 _ 高斯 _）分布的很好例子。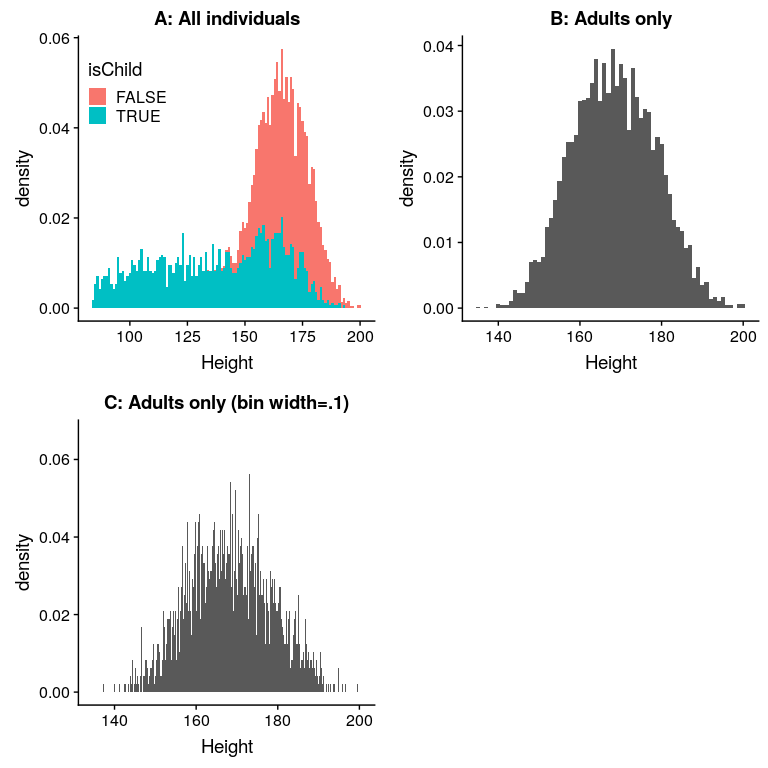  图 4.5 nhanes 高度柱状图。A：分别为儿童（蓝色）和成人（红色）绘制的值。B：仅限成人使用。C:与 B 相同，但仓宽=0.1 ### 4.2.4 柱状图箱 在我们前面使用睡眠变量的例子中，数据是以整数报告的，我们只计算报告每个可能值的人数。但是，如果您查看 nhanes 中高度变量的一些值，您将看到它是以厘米为单位测量的，一直到小数点后一位： ```r # take a slice of a few values from the full data frame NHANES_adult %>% dplyr::select(Height) %>% slice(45:50) %>% pander() ``` <colgroup><col style="width: 11%"></colgroup> | 高度 | | --- | | 169.6 条 | | 169.8 条 | | 167.5 条 | | 155.2 条 | | 173.8 条 | | 174.5 条 | 图[4.5](#fig:heightHistSep)的面板 C 显示了统计每个可能值的密度的直方图。这个柱状图看起来真的参差不齐，这是因为特定的小数位值的可变性。例如，值 173.2 出现 32 次，而值 173.3 只出现 15 次。我们可能不认为这两个权重的流行率真的有如此大的差异；更可能的原因是我们的样本中的随机变异性。 一般来说，当我们创建一个连续的或可能有很多值的数据柱状图时，我们将 _bin_ 这些值，这样我们就不会计算和绘制每个特定值的频率，而是计算和绘制特定范围内的值的频率。e.这就是为什么上面[4.5](#fig:heightHistSep)的面板 B 中的图看起来不那么锯齿状的原因；如果您查看`geom_histogram`命令，您将看到我们设置了“b in width=1”，它告诉命令通过将 b in 中的值与宽度为 1 的值组合来计算柱状图；因此，值 1.3、1.5 和 1.6 would 所有数据都计算在同一个存储单元的频率上，从等于 1 的值到小于 2 的值。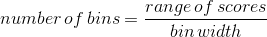  请注意，一旦选择了箱大小，则箱的数量将由数据确定： 如何选择最佳的仓宽没有硬性和快速性的规则。偶尔它会很明显（就像只有几个可能的值一样），但在许多情况下，它需要反复尝试。有一些方法试图找到一个最佳的仓位大小，例如在 r 的`nclass.FD()`函数中实现的 freedman diaconis 方法；我们将在下面的一些示例中使用该函数。