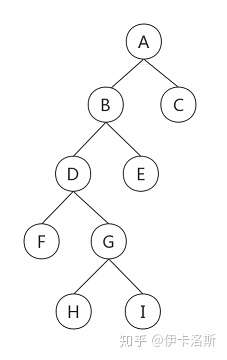
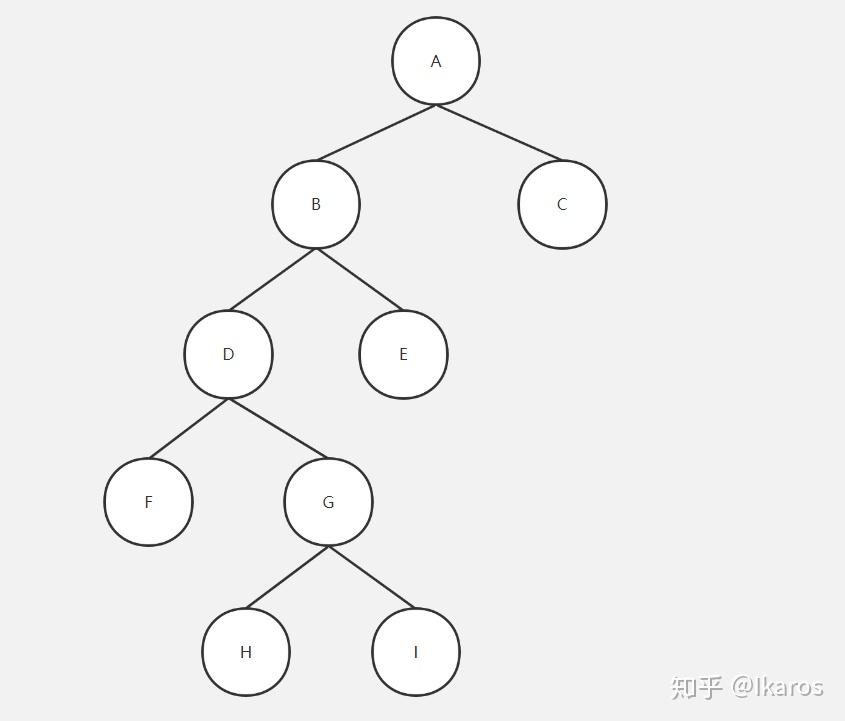
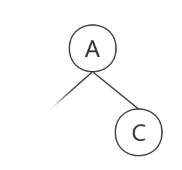
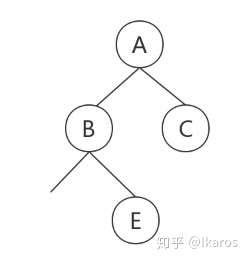
二叉树：  前序遍历A-B-D-F-G-H-I-E-C 中序遍历F-D-H-G-I-B-E-A-C 后序遍历F-H-I-G-D-E-B-C-A **前序(根左右)，中序(左根右)，后序(左右根)** 例题1: 已知某二叉树的前序遍历为A-B-D-F-G-H-I-E-C,中序遍历为F-D-H-G-I-B-E-A-C,请还原这颗二叉树。 解题思路： 从前序遍历中，我们确定了根结点为A，在从中序遍历中得出 F-D-H-G-I-B-E在根结点的左边，C在根结点的右边，那么我们就可以构建我们的二叉树的雏形。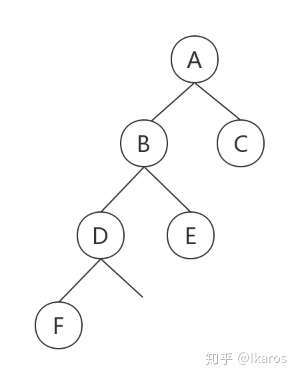  那么剩下的前序遍历为B-D-F-G-H-I-E，中序遍历为F-D-H-G-I-B-E， B就是我们新的“根结点”，从中序遍历中得出F-D-H-G-I在B的左边，E在B的右边，继续构建  那么剩下的前序遍历为D-F-G-H-I，中序遍历为F-D-H-G-I，D就是我们新的“根结点”，从中序遍历中得出F在D的左边，H-G-I在D的右边，继续构建  那么剩下的前序遍历为G-H-I，中序遍历为H-G-I，G就是我们新的“根结点”，从中序遍历中得出H在G的左边，I在G的右边，继续构建  例题2： 已知某二叉树的中序遍历为F-D-H-G-I-B-E-A-C,后序遍历为F-H-I-G-D-E-B-C-A,请还原这颗二叉树。 解题思路： 从后序遍历中，我们确定了根结点为A，在从中序遍历中得出 F-D-H-G-I-B-E 在根结点的左边，C在根结点的右边，那么我们就可以构建我们的二叉树的雏形。之后就是新根节点B，FDHGI在根左，E在根右。在之后就是新根D，F根左，HGI根右，然后就差不多了。 和前序和中序还原二叉树一样，我们同理可以通过中序和后序还原二叉树。  **光有前序遍历和后序遍历是无法还原二叉树的。**