0221. 最大正方形 · ttttt

# 0221. 最大正方形 ## 题目地址(221. 最大正方形) <https://leetcode-cn.com/problems/maximal-square/> ## 题目描述 ``` <pre class="calibre18">``` 在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。示例: 输入: 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 输出: 4 ``` ``` ## 前置知识 - 动态规划 - 递归 ## 公司 - 阿里 - 腾讯 - 百度 - 字节 ## 思路 ![](https://img.kancloud.cn/1f/cd/1fcd397f463f55fad67e330b2a07e24a_420x355.jpg) 符合直觉的做法是暴力求解处所有的正方形，逐一计算面积，然后记录最大的。这种时间复杂度很高。我们考虑使用动态规划，我们使用dp\[i\]\[j\]表示以matrix\[i\]\[j\]为右下角的顶点的可以组成的最大正方形的边长。那么我们只需要计算所有的i，j组合，然后求出最大值即可。我们来看下dp\[i\]\[j\] 怎么推导。首先我们要看matrix\[i\]\[j\], 如果matrix\[i\]\[j\]等于0，那么就不用看了，直接等于0。如果matrix\[i\]\[j\]等于1，那么我们将matrix\[\[i\]\[j\]分别往上和往左进行延伸，直到碰到一个0为止。如图 dp\[3\]\[3\] 的计算。 matrix\[3\]\[3\]等于1，我们分别往上和往左进行延伸，直到碰到一个0为止，上面长度为1，左边为3。 dp\[2\]\[2\]等于1（之前已经计算好了），那么其实这里的瓶颈在于三者的最小值, 即`Min(1, 1, 3)`, 也就是`1`。那么dp\[3\]\[3\] 就等于 `Min(1, 1, 3) + 1`。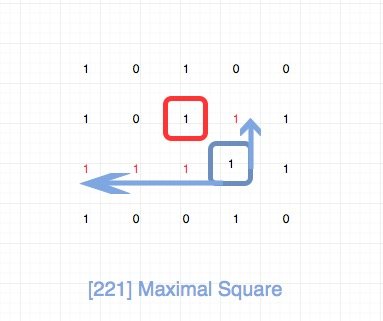 ![](https://img.kancloud.cn/84/59/8459a651d6f2b68dde7e87cfaaf02519_383x321.jpg) dp\[i - 1\]\[j - 1\]我们直接拿到，关键是`往上和往左进行延伸`, 最直观的做法是我们内层加一个循环去做就好了。但是我们仔细观察一下，其实我们根本不需要这样算。我们可以直接用dp\[i - 1\]\[j\]和dp\[i\]\[j -1\]。具体就是`Min(dp[i - 1][j - 1], dp[i][j - 1], dp[i - 1][j]) + 1`。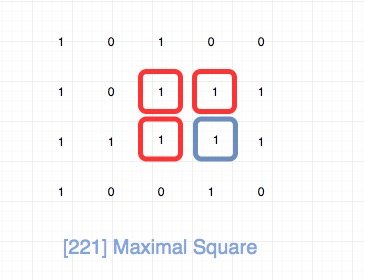 ![](https://img.kancloud.cn/fe/84/fe84a3d7426b688b280cc40dec967bbf_365x280.jpg) 事实上，这道题还有空间复杂度O(N)的解法，其中N指的是列数。大家可以去这个[leetcode讨论](https://leetcode.com/problems/maximal-square/discuss/61803/C%2B%2B-space-optimized-DP)看一下。 ## 关键点解析 - DP - 递归公式可以利用dp\[i - 1\]\[j\]和dp\[i\]\[j -1\]的计算结果，而不用重新计算 - 空间复杂度可以降低到O(n), n为列数 ## 代码代码支持：Python，JavaScript： Python Code： ``` <pre class="calibre18">``` class Solution: def maximalSquare(self, matrix: List[List[str]]) -> int: res = 0 m = len(matrix) if m == 0: return 0 n = len(matrix[0]) dp = [[0] * (n + 1) for _ in range(m + 1)] for i in range(1, m + 1): for j in range(1, n + 1): dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1 if matrix[i - 1][j - 1] == "1" else 0 res = max(res, dp[i][j]) return res ** 2 ``` ``` JavaScript Code： ``` <pre class="calibre18">``` /* * @lc app=leetcode id=221 lang=javascript * * [221] Maximal Square */ /** * @param {character[][]} matrix * @return {number} */ var maximalSquare = function(matrix) { if (matrix.length === 0) return 0; const dp = []; const rows = matrix.length; const cols = matrix[0].length; let max = Number.MIN_VALUE; for (let i = 0; i < rows + 1; i++) { if (i === 0) { dp[i] = Array(cols + 1).fill(0); } else { dp[i] = [0]; } } for (let i = 1; i < rows + 1; i++) { for (let j = 1; j < cols + 1; j++) { if (matrix[i - 1][j - 1] === "1") { dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1; max = Math.max(max, dp[i][j]); } else { dp[i][j] = 0; } } } return max * max; }; ``` ``` ***复杂度分析*** - 时间复杂度：O(M∗N)O(M \* N)O(M∗N)，其中M为行数，N为列数。 - 空间复杂度：O(M∗N)O(M \* N)O(M∗N)，其中M为行数，N为列数。